concours électroradiologie médicale de l'uranium au plomb : âge d'une roche ancienne. Tours 2007

sans calculatrice

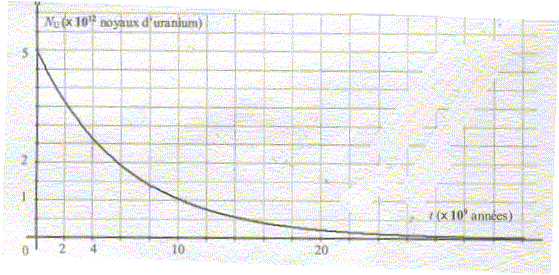
A. de l'uranium 238 au plomb 206 :

Rappeler les lois de conservations vérifiées lors d'une réaction nucléaire.

Dans la première étape, un noyau ²³⁸₉₂U subit une désintégration de type a. Le noyau fils est du thotium ( Th). Ecrire l'équation de cette réaction nucléaire.

Dans la seconde étape, le noyau de thorium 234 se transforme en un noyau de proactinium ²³⁴₉₁Pa. Ecrire l'équation de cette réaction nucléaire. Quel est le type de radioactivité correspondante ?

L'équation globale du processus de transformation d'un noyau d'uranium 238 en un noyau de plomb est :

²³⁸₉₂U --> ²⁰⁶₈₂Pb + x a + y b.

Déterminer x et y.

B. Datation :

On a constaté, d'une part que le minéraux d'une même couche géologique, donc du même âge, contiennet de l'uranium 238 et du plomb en proportions remarquablement constantes et, d'autre part que la quantité de plombdans le minéral augmente avec l'âge.

Si on mesure la quantité de plomb 206 dans un échantillon de roches anciennes, en considérant qu'il n'y en avait pas initialement, on peut déterminer l'âge du minéral à partir de la courbe de décroissance radioactive du nombre de noyaux d'uranium 238.

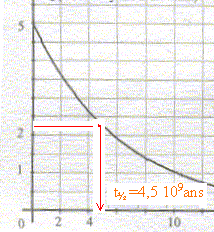
Définir le temps de demi-vie t_½ de l'uranium 238. Le déterminer graphiquement.

Donner l'expression de N_U(t) , le nombre de noyaux radioactifs présents dans l'échantillons à la date t, en fonction de N_U(0) et de la constante radioactive l.

Etablir la relation entre l et t_½.

A partir de l'équation de la transformation globale précédente, exprimer :
- N_Pb(t) en fonction de N_U(t) et de N_U(0), en faisant l'hypothèse que les noyaux intermédiaires de la famille sont en quantité négligeable.

- N_Pb(t) en fonction de t, l, N_U(t).

Exprimer l'âge de la roche en fonction de t_½ et du rapport N_Pb(t) / N_U(t).

Déterminer l'âge de la roche si N_Pb(t) / N_U(t) = 1,2 10^-2.

ln(1,2 10^-2) = -4,4 ; ln 1,012 = 1,2 10^-2 ; ln2 = 0,69 ; 4,4*4,5/0,69 = 29 ; 4,4*4,4/0,69 = 28 ; 1,2*4,5/0,69 = 7,8 ; 1,2*4,4/0,69 = 7,7

Lois de conservations vérifiées lors d'une réaction nucléaire.

Conservation de la charge, du nombre de nucléons et de la grandeur masse énergie.

Dans la première étape, un noyau ²³⁸₉₂U subit une désintégration de type a. Le noyau fils est du thotium ( Th).

²³⁸₉₂U -->²³⁴₉₀Th + ⁴₂He

Dans la seconde étape, le noyau de thorium 234 se transforme en un noyau de proactinium ²³⁴₉₁Pa.

²³⁴₉₀Th -->²³⁴₉₁Pa + ⁰_-1e : type b^-.

conservation du nombre de nucléons : 238 = 206 + 4x soit x= 8.

conservation de la charge : 92 = 82 + 2x-y soit 10=2x-y d'où y = 6.

B. Datation :

temps de demi-vie t_½ : durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.

loi de décrioissance radioactive : N_U(t) = N_U(0) exp(-lt) soit N_U(0) = N_U(t) exp(lt)

Nombre de noyaux radioactifs présents dans l'échantillons à la date t :

N_U(t) = N_U(0) exp(-lt)

Relation entre l et t_½.

N_U(t_½) = 0,5 N_U(0) = N_U(0) exp(-lt_½)

0,5 = exp(lt_½) ; ln 0,5 = -lt_½ ; lt_½ = ln 2.

N_Pb(t) en fonction de N_U(t) et de N_U(0) :

N_Pb(t) = N_U(0) -N_U(t)

N_Pb(t) en fonction de t, l, N_U(t) :

N_U(0) -N_U(t) ; N_U(0) = N_U(t) exp(lt )

N_Pb(t) = N_U(t)( exp(lt)-1)

âge de la roche en fonction de t_½ et du rapport N_Pb(t) / N_U(t).

N_Pb(t) / N_U(t) = exp(lt)-1 avec lt_½ = ln 2.

1+N_Pb(t) / N_U(t) = exp(lt) ; ln(1+N_Pb(t) / N_U(t))= lt ;

t= ln(1+N_Pb(t) / N_U(t))/l ;

t= ln(1+N_Pb(t) / N_U(t))/ ln2 t_½.

si N_Pb(t) / N_U(t) = 1,2 10^-2.

t = ln( 1+0,012) / 0,69 * 4,5 10⁹ =1,2 10^-2/0,69* 4,5 10⁹ = 7,8 10⁷ années.