Principe de la mesure de la valeur efficace d'une tension périodique concours technicien laboratoire 2007

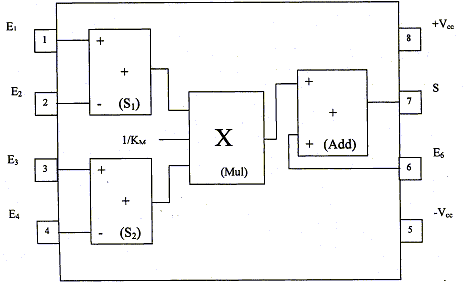
Le premier étage ( le multiplieur ) élève v(t) au carré, le deuxième étage ( le filtre passe bas) en retite la valeur moyenne, le dernier étage extrait la racine carrée.

On supposera que tous les circuits intégrés utilisés sont idéaux :

les intensités des courants d'entrée sont nulles ; la résistance de sortie est nulle ; les A.O fonctionnent en régime linéaire, leur tension différentielle d'entrée U_d est donc nulle.

Etude du multiplieur analogique :

Son shéma fonctionnel et son brochage sont donnés ; S₁ et S₂ effectuent chacun une soustraction, Mul effectue une multiplication avec la constante 1/K_m et Add effectue une addition.

.

On note v_E1(t), v_E2(t)...v_E6(t) les tensions instantanées appliquées respectivement sur les entrées E₁, E₂....E₆ et on note v_s(t) la tension de sortie S. On a ainsi :

v_s(t) = (1/K_m) [ v_E1(t)- v_E2(t)] [ v_E3(t)- v_E4(t)] + v_E6(t)

On veut que la tension de sortie v_s(t) soit telle que : v_s(t) =k v_E1(t) v_E3(t).

- Quelles sont les bornes d'entrée qu'il faut relier à la masse ?

- Quelle relation a t-on entre k et K_m ?

- Calculer K_m si k = 0,1 V^-1. 

identifier à : v_s(t) =k v_E1(t) v_E3(t).

ce qui entraîne : v_E2(t) = 0 ; v_E4(t) = 0 ; v_E6(t) = 0 soit E₂, E₄ et E₆ reliées à la masse.

k = 1/K_m soit K_m = 1/k = 1/0,1 = 10.

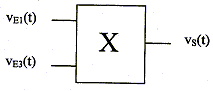
On applique sur les deux entrées des tensions v_E1(t) et v_E3(t) continues constantes de valeurs respectives V_E1 = 5 V et V_E3 = 8 V.

Quelle type de tension v_s(t) recueille t-on en sortie ? Quelle est sa valeur numérique ?

réponse :

v_s(t) =k v_E1(t) v_E3(t) = 0,1V_E1V_E3 =0,1*5*8 =4 V.

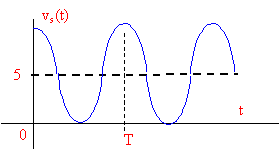
Rappel : cos a cos b = ½[cos ( a+b) + cos (a-b)]

Exprimer v_s(t) et montrer que v_s(t) peut s'écrire v_s(t) = 5[1+ cos(2wt) ]en volts.

Tracer l'allure approximative de v_s(t) et calculer sa valeur moyenne <v_s(t)>.

réponse :

v_s(t) =k v_E1(t) v_E3(t) =k V²cos (wt) V cos (wt)

v_s(t) =½k V² [cos (wt +wt) +cos(wt-wt)]

v_s(t) =½k V²[cos (2wt) +cos(0)]

v_s(t) =½k V²[cos (2wt) +1] = 0,5*0,1*10²[cos (2wt) +1]

v_s(t) = 5[1+ cos(2wt) ].

valeur moyenne <v_s(t)> :

La valeur moyenne de cos (2wt) est nulle ; la valeur moyenne de v_s(t) vaut : <v_s(t) > = 5 V.