Aurélie 3/0507
 

Concours kiné Rennes : oscillations mécaniques 2007

Google

 

Les vecteurs sont écrits en gras et en bleu.

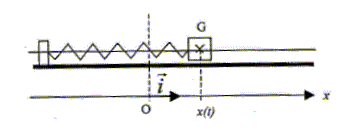
Etude théorique d'un oscillateur mécanique horizontal ( 5 pts)

Les frottements sont négligés dans cette partie.

Un système solide-ressort est constitué d'un solide de masse m=100 g mobile sur un support horizontal et fixé à l'extrémité d'un ressort à spires non jointives, de masse négligeable et de constante de raideur k =4 N/m. Le solide est mis en mouvement en le déplaçant de sa position d'équilibre, position pour laquelle l'abscisse x du centre d'inertie G est nulle.

  1. Représenter les forces s'exerçant sur le solide et les nommer.
  2. Etablir l'équation différentielle du mouvement du centre d'inertie G du solide.
    La solution générale de l'équation différentielle est de la forme x(t) =xm cos (2    pt/T0+j)
  3. Déterminer l'expression de la période propre T0 de l'oscillateur et vérifier son homogénéité par une analyse dimensionnelle. Faire l'application numérique.
  4. Exprimer l'énergie mécanique Em du système solide-ressort étudié dans une position d'abscisse x, en fonction de m, k, x et v, valeur de la vitesse du centre d'inertie G.
  5. Démontrer que l'énergie mécanique est constante en établissant son expression en fonction de k et xm.
 Etude expérimentale de oscillateur mécanique horizontal

Le système solide-ressort oscille en présence de frottement.

  1. Nommer le régime des oscillations et le temps caractéristique T correspondant. Déterminer T et comparer à T0.
  2. Calculer la valeur de l'énergie mécanique à t=0 et en déduire l'échelle en ordonnée.
  3. Attribuer aux courbes 1, 2 et 3 l'énergie Ec, Ep, Em correspondante. Justifier.
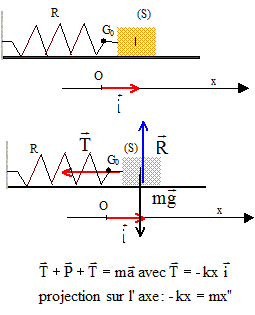
Etude théorique d'un oscillateur mécanique horizontal:

Les forces s'exerçant sur le solide :

Poids, verticale vers le bas, valeur mg

Action du plan, verticale, vers le haut, opposée au poids.

Tension du ressort, horizontale, dirigé vers O, valeur k|x|

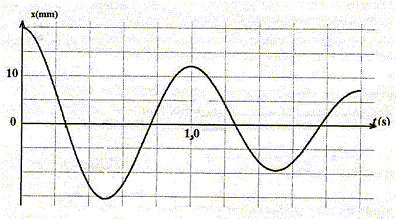
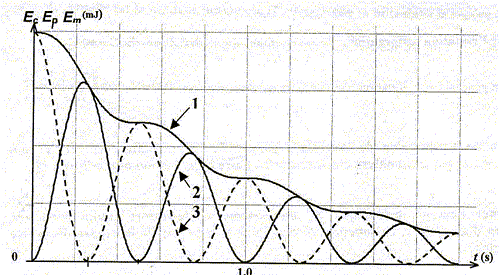
Equation différentielle du mouvement du centre d'inertie G du solide :

mx"+kx=0 ; x" + k/m x=0

On pose w02=k/m ; x" +w02=0 (1)

La solution générale de l'équation différentielle est de la forme x(t) =xm cos (2pt/T0+j)

Expression de la période propre T0 de l'oscillateur :

x'(t) = -xm2p/T0 sin (2pt/T0+j)

x"(t) = -xm[2p/T0]2cos (2pt/T0+j) = -[2p/T0]2 x(t)

repport dans l'équation différentielle :

-[2p/T0]2 x(t) +k/m x(t) = 0

Egalité vérifiée quelque soit t si : [2p/T0]2 =k/m soit T0 = 2p[m/k]½.

T0 =6,28[0,1/4]½ ; T0 =0,99 s.

Homogénéité de la période :

2pest sans dimension ; [m] = M ( masse ) ;

k raideur , force / longueur ; force = masse * accélération = masse * longueur / temps2 ;

[k]=M T-2 ; [1/k]= M-1 T2 ; [m/k] = T2 ; [m/k] ½= T.

Energie mécanique Em du système solide-ressort étudié dans une position d'abscisse x :

L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle élastique.

L'origine de l'énergie potentielle est prise à la position d'équilibre.

Em = ½kx2 + ½mv2.

En absence de frottement l'énergie mécanique est constante :

Lorsque x(t) = xm, la vitesse est nulle et l'énergie mécanique est sous forme d'énergie potentielle élastique.

Em= ½kxm2.

 Etude expérimentale de oscillateur mécanique horizontal

Le régime des oscillations : pseudopériodique.

Le temps caractéristique T vaut T=1,0 s. (lecture graphe)

A 1 % près T est égale à T0.

Valeur de l'énergie mécanique à t=0 : x(0)= xm = 20 mm = 0,02 m

Lorsque x(t) = xm, la vitesse est nulle et l'énergie mécanique est sous forme d'énergie potentielle élastique.

Em= ½kxm2 = 0,5*4*0,022 = 8 10-4 J.

Echelle en ordonnée : 1 division correspond à 2 10-4 J.

Courbe 3 : énergie potentielle élastique ( à t=0, x=xm et l'énergie mécanique est sous forme potentielle élastique)

courbe 2 : énergie cinétique ( à t = 0, la vitesse est nulle)

courbe 1 : énergie mécanique ( somme de l'énergie potentielle et de l'énergie cinétique)

 
 

retour -menu