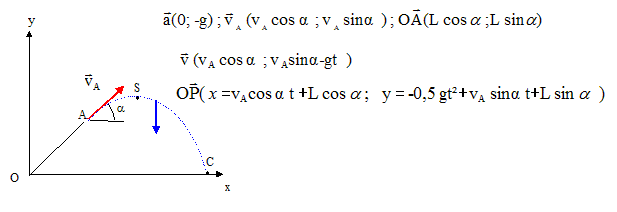Aurélie 3/05/07
 

Concours kiné Rennes : mouvement d'une bille 2007

Google

 

Les vecteurs sont écrits en gras et en bleu.

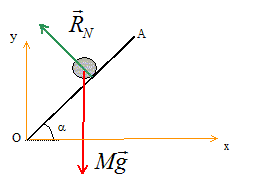
On admet que la bille est assimilée à un point matériel et se déplace sans frottement sur le rail. g = 9,8 m/s2.

Un jouet d'enfant est constitué d'une bille lancée avec une vitesse initiale v0 à l'aide d'un ressort actionné par le joueur sur un rail rectiligne, orientable, de longueur L= 20 cm. Ce rail est disposé dans un plan vertical rapporté au repère (O, x, y). L'axe Ox est horizontal et l'axe Oy vertical dirigé vers le haut. Le rail fait un angle a avec le sol (Ox). La bille, notée B, se trouve à l'instant initial t0 du lancement au point O(0,0), origine du repère. Elle se déplace sur le rail et atteint l'extrémité supérieure A du rail à la date tA, avec une vitesse vA de valeur 1,0 m/s lorsque a=50°. Elle tombe ensuite en chute libre.

  1. Faire le schéma de la situation décrite en représentant l'origine et les axes du repère, le rail, l'angle a, la bille entre les dates t0 et tA, ainsi que les forces auxquelles elle est soumise.
  2. Calculer la valeur de la vitesse v0 de la bille lors de son lancement.
  3. Déterminer les équations horaires de la bille en chute libre dans le repère (O, x, y) en prenant l'instant tA comme origine des dates.
  4. Quelle est la hauteur maximale atteinte par la bille ?
  5. A quelle distance du point O, la bille retombe t-elle au sol ?
Schéma de la situation décrite :

 

Valeur de la vitesse v0 :

Théorème de l'énergie cinétique entre le point O et le point A.

L'action du plan, perpendiculaire à la vitesse ne travaille pas.

Le travail du poids est résistant en montée et vaut : -MgL sin a.

Variation de l'énergie cinétique : ½MvA2- ½Mv02.

½MvA2- ½Mv02 = -MgL sin a.

v02 =vA2+ 2gLsin a ; v0 =[vA2+ 2gLsin a]½.

v0 =[1+ 2*9,8*0,2 sin 50]½ ; v0 = 2,0 m/s.

 
Equations horaires de la bille en chute libre dans le repère (O, x, y) en prenant l'instant tA comme origine des dates :

Hauteur maximale atteinte par la bille :

Au point S la vitesse est horizontale et vaut vA cos a.

La composante verticale de la vitesse est nulle : vA sin a-gtS=0; tS = vA sin a/g

repport dans y : yS= -0,5g[vA sin a/g]2+[vA sin a]2/g +Lsin a.

yS=0,5[vA sin a]2/g +Lsin a.

yS=0,5[ sin 50 ]2/9,8 +0,2 sin 50 ; yS=0,18 m

 

A quelle distance du point O, la bille retombe t-elle au sol ?

Au point C, yC=0

-0,5 gt2 + vA sin a t +Lsin a=0

-4,9 t2 +0,766 t +0,153 =0

résoudre : t = 0,271 s.

repport dans x : xC= vA cos a t + Lcos a.

xC= cos50*0,271 + 0,2 *cos50 ; xC=0,30 m.

 
 

retour -menu