Aurélie 22/05/07
 

concours électroradiologie médicale diffraction ( lumière) ; oscillateur élastique. Poitiers 2007

Google

 

Ondes lumineuses : (5 points)

Un laser émet une lumière monochromatique de longueur d'onde dans le vide l = 650 nm.

  1. Quelle est la fréquence de cette radiation ? Cette fréquence change t-elle lorsque la radiation passe dans du verre ? c = 3,0 108 m/s.
  2. Le faisceau lumineux traverse une fente de largeur a.

    La largeur de la tache centrale vaut d = 13 mm.
    Sur l'écran placé à la distance D de la fente on observe une tache centrale, de largeur d, étalée dans la direction perpendiculaire à la fente, et symétriquement, de part et d'autre de la tache centrale, d'autres taches moins lumineuses et plus petites.
  3. Quel est le nom du phénomène observé ? Quelle condition doit satisfaire la largeur de la fente pour obtenir cette figure ?
  4. On appelle q, l'écart angulaire entre le centre de la tache centrale et la première extinction. En considérant cet angle faible, établir la relation entre q, D et d.
  5. On recommence l'expérience en utilisant la même fente, la distance D est conservée mais la lumière utilisée a une longueur d'onde inconnue, notée l1. La largeur de la tache centrale de la figure observée vaut d1 = 9,2 mm.
    - Déterminer     l1 ; quelle est la couleur correspondant à cette radiation ?
    - Décrire et justifier le plus précisément possible la figure obtenue si on utilisait une lumière polychromatique pour réaliser cette expérience.
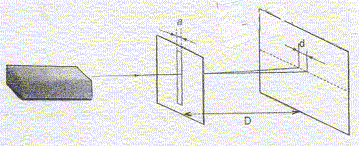
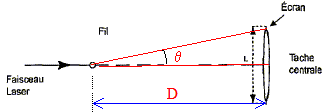
Un laser émet une lumière monochromatique de longueur d'onde dans le vide l = 650 nm.

Fréquence de cette radiation :

f = c/l = 3 108 / 650 10-9 = 4,6 1014 Hz.

Cette fréquence est une caractéristique de l'onde : elle rete constante quel que soit le milieu de propagation..

Le faisceau lumineux traverse une fente de largeur a. :

on observe un phénomène de diffraction dans la mesure ou la largeur de la fente est du même ordre de grandeur que la longueur d'onde.

q = l/a.

avec : l longueur d'onde (m) et a : largeur de la fente (m)

Relation entre q, D et d :

Sur le schéma on note L la largeur de la tache centrale : L= d = 13 mm

tan q = ½L/D voisin de q radian pour les angles petits.

q = ½L/D ou q = ½d/D

 

On recommence l'expérience en utilisant la même fente, la distance D est conservée mais la lumière utilisée a une longueur d'onde inconnue, notée l1. La largeur de la tache centrale de la figure observée vaut d1 = 9,2 mm.

Calcul de l1 :

q = ½d/D

Et en tenant compte du fait que q = l/a il vient :

l = a/(2D) d ; a/(2D) est une constante : l et d sont proportionnels

l1 =d1/d l = 9,2/13*650 = 460 nm.
La couleur correspondant à cette radiation est le bleu.
Figure obtenue si on utilisait une lumière polychromatique pour réaliser cette expérience :

Chaque radiation de la lumière polychromatique donne un système de diffraction dont la largeur de la tache centrale est proportionnelle à la longueur d'onde. A centre de la tache toutes les radiations sont présentes ( couleur blanche) ; le bord de la tache centrale est orange-rouge, le bleu étant absent .

Oscillateur élastique ( 5 points)

Le dispositif ci-dessous est constitué d'un ressort de constante de raideur k = 5,0 N/m et d'un corps solide de masse m = 500 g qui se déplace sur un banc à coussin d'air ( ce qui rend les frottements négligeables). Le point O est pris à la position occupée par le centre d'inertie G du solide lorsque le dispositif est au repos, la soufflerie fonctionnant. On écarte le corps de 4,0 cm vers la droite à l'instant t=0 et on le lance dans le sens xx' avec une vitesse vini = - 30,0 cm/s.

  1. Effectuer le bilan des actions qui s'exercent sur le solide :
    - lorsque le dispositif est au repos, soufflerie en action.
    - lorsque le dispositif est en mouvement.
  2. Etablir l'équation différentielle qui régit le mouvement de l'oscillateur au cours du temps.
  3. La solution de l'équation différentielle est du type x(t) = Xmax cos(2pt/T0+j)
    - Vérifier que cette fonction est bien solution de l'équation différentielle.
    - En déduire que l'expression de T0= 2p(m/k)½. En effectuant une analyse dimensionelle, justifier que T0 est homogène à un temps. Comment nomme t-on T0 ?
    - Préalablement à l'expérience décrite ci-dessus, on avit chronomètré la durée de 15 oscillations du dispositif et on avit trouvé Dt = 29,5 s. Ce résultat est il en accord avec le calcul.
    - Déterminer Xmax, et j après avoir rappelé les noms de ces grandeurs.
  4. Définir l'énergie mécanique de l'oscillateur à une date t quelconque et donner son expression littérale. Que vaut numériquement cette énergie et sous quelle forme se trouve t-elle lorsque x = Xmax ?
 

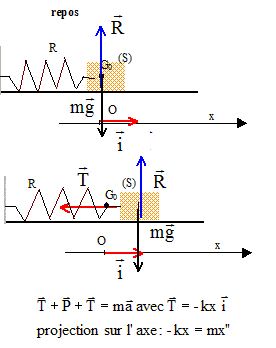
L'équation différentielle peut s'écrire : x" + k/m x=0 (1)

La solution de l'équation différentielle est du type x(t) = Xmax cos(2pt/T0+j)
Vérifions que cette fonction est bien solution de l'équation différentielle.

dériver deux fois x(t) par rapport au temps :

x' = -Xmax2p/T0 sin(2pt/T0+j)

x" = -Xmax(2p/T0 )2 cos(2pt/T0+j)

repport dans l'équation différentielle (1):

-Xmax(2p/T0 )2 cos(2pt/T0+j) + k/m Xmax cos(2pt/T0+j) =0

Cette égalité est vérifiée quelque soit le temps si : (2p/T0 )2 = k/m

soit T0 = 2p(m/k)½.
En effectuant une analyse dimensionelle, justifions que la période T0 est homogène à un temps.

2p est sans dimension ; m est une masse : [m]= M.

k est une raideur, une force divisée par une longueur ; or une force est une masse fois une accélération ; une accélération est un longueur divisée par un temps au carré.

D'où : [k]= M T-2 ; [m/k]= T2 ; [m/k]½= T.


- Préalablement à l'expérience décrite ci-dessus, on avait chronomètré la durée de 15 oscillations du dispositif et on avait trouvé Dt = 29,5 s.

Texp= 29,5/15 =1,967 s. ( 2,0 s)

T0 = 2p(m/k)½=6,28 (0,5/5)½ =1,985 s ( ( 2,0 s)

Ces résultat sont en accord.
Déterminons Xmax, et j après avoir rappelé les noms de ces grandeurs.

Xmax : amplitude en mètre ; j : phase à la date t=0 en radian.

x(0) = Xmax cosj ; x(0) = 0,04 m ; 0,04 = Xmax cosj (2).

vitesse x'(t) = -Xmax2p/T0 sin(2pt/T0+j)

v'(0) = -Xmax2p/T0 sin j ; v'(0) = -0,30 m/s ; 0,3 = Xmax2p/T0 sin j

2p/T0 = (k/m)½ = (5/0,5)½ =3,16 ; 0,3 = 3,16 Xmaxsin j ; 9,49 10-2 = Xmaxsin j (3)

(3) sur (2) donne : 9,49 10-2 / 0,04= tan j ; j = 1,17 rad (j =1,2 rad)

0,04 /cosj = Xmax = 0,04 /cosj =0,04/0,388 = 0,103 m ; Xmax = 0,10 m.

L'énergie mécanique de l'oscillateur à une date t quelconque est la somme de l'énergie potentielle élastique et de l'énergie cinétique :

E= ½kx2 +½mv2.

E= ½kX2max cos2(2pt/T0+j) + ½mX2max(2p/T0 ) 2 sin2(2pt/T0+j)

Or m(2p/T0 ) 2 = k ;

E= ½kX2max cos2(2pt/T0+j) + ½kX2max sin2(2pt/T0+j) ; E= ½kX2max.

E= 0,5*5*0,1032 = 0,026 J.

Lorsque x = Xmax , la vitesse est nulle : l'énergie se trouve sous forme potentielle élastique.

 

retour -menu