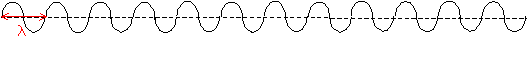|
concours orthoptie
ondes sur une corde ;
radioactivité : radium, radon .
Nantes
2004
|
|||
|
|||
|
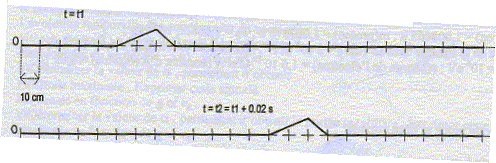
Vitesse de propagation de la déformation : La déformation parcourt d = 80 cm = 0,8 m en t2-t1 = 20 ms = 0,02 s. ( lecture graphe) v= d / ( t2-t1 ) = 0,8 / 0,02 ; v= 40 m/s. Date t1 : A la date t1, la déformation a parcouru 0,8 m ( lecture graphe). t1 =0,8/40 ; t1 = 20 ms. La corde à la date t3=35 ms :
Tension de la corde : v = [T/m]½ avec T: tension (N) et m =5 10-3 kg m-1 : masse linéique de la corde. T = v2m = 402*5 10-3 ; T= 8 N. On génère maintenant
en continu au point O une onde sinusoïdale de
fréquence f = 200 Hz. Longueur de la corde : L= 2,4 m.
Valeur de la fréquence des éclairs fs pour laquelle on visualise une seule corde immobile : 200 Hz ou un sous multiple de 200
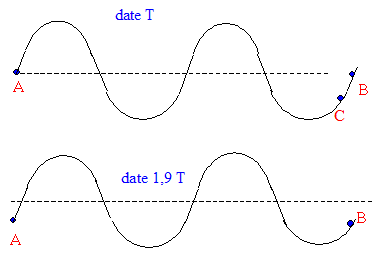
Hz : 100, 50, 25 Hz. période de l'onde sinusoïdale : T = 1/200 = 5 ms Ts = 1/105 =9,5 ms = 9,5/5 = 1,9 T.
A la date t =1,9 T, le point B se retrouve à la place occupée précédemment par le point C : Le mouvement apparent est donc en sens contraire du mouvement réel. La vitesse s'effectue le mouvement apparent de propagation de l'onde le long de la corde est : B et C sont distants de 0,1 l= 0,02 m v apparente = 0,02 / 9,510-3 = 2,1 m/s.
Radioactivité : Les noyaux de radium 22688Ra se désintègrent spontanément en donnant un noyau de radon 22286Rn avec un temps de demi-vie t½.
m(22688Ra) = 225,9791 u ; m(22286Rn) = 221,9703 u ; m(42He) = 4,00150 u ; m(neutron) = 1,008665 u ; m(proton) = 1,007276 u ; 1 u = 1,66606 10-27 kg.
Equation de désintégration du radium : 22688Ra --->22286Rn + 42He type de radioactivité : a. Energie dégagée par cette désintégration : Dm = m(42He) + m(22286Rn) - m(22688Ra) Dm = 4,00150 +221,9703-225,9791 = -0,0073 u = -0,0073*1,66606 10-27 =-1,216 10-29 kg. DE = Dm c2 =-1,216 10-29 *9 1016 =-1,09 10-12 J. Vitesse des particules a émises lors de cette désintégration : ½m(42He)v2 = |DE| ; v = [2|DE| /m(42He)]½ = [2*1,09 10-12/(4,0015*1,666 10-27) ]½ =1,81 107 m/s. Certaines désintégrations s'accompagnent de l'émission d'un rayonnement g de longueur d'onde l = 6,54 10-12 m. Le noyau fils se trouve dans un état excité : le retour à l'état fondamental de moindre énergie s'accompagne de l'émission d'un photon g. Energie du photon g : E= hc/l. E = 6,63 10-34*3 108/6,54 10-12 = 3,04 10-14 J Energie cinétique du noyau d'hélium : 1,09 10-12 - 3,04 10-14 = 1,06 10-12 J Vitesse des particules a émises lors de cette désintégration : ½m(42He)v2 = |DE| ; v = [2|DE| /m(42He)]½ = [2*1,06 10-12/(4,0015*1,666 10-27) ]½ =1,78 107 m/s. Energie de liaison par nucléon en MeV pour un noyau de radium : 88 protons et 226-88 = 138 neutrons. Dm = 88m(proton) + 138 m(neutron) -m(22688Ra) Dm = 88*1,007276+138*1,008665-225,9791 =1,8569 u = 1,8569*1,666 10-27 = 3,09 10-27 kg El = Dm c2 = 3,09 10-27 * 9 1016 = 2,784 10-10 J = 2,784 10-10/ 1,60 10-13 = 1740 MeV. El /A = 1740 / 226 = 7,70 MeV/nucléons. Energie de liaison par nucléon en MeV pour un noyau de radon : 86 protons et 222-86 = 136 neutrons. Dm = 86m(proton) + 136 m(neutron) -m(22286Rn) Dm = 86*1,007276+136*1,008665-221,9703 =1,8338 u = 1,8338*1,666 10-27 = 3,055 10-27 kg El = Dm c2 = 3,055 10-27 * 9 1016 = 2,75 10-10 J = 2,784 10-10/ 1,60 10-13 = 1718 MeV. El /A = 1718 / 222 = 7,74 MeV/nucléons. Cette valeur est supérieure à celle du noyau de radium : le noyau fils est plus stable que le noyau initial ; la désintégration du radium est spontanée. Energie de liaison par nucléon en MeV pour un noyau d'hélium : 2 protons et 2 neutrons. Dm =2 m(proton) + 2 m(neutron) -m(42He) Dm = 2*1,007276+2*1,008665-4,0015 =0,034 u = 0,034*1,666 10-27 = 5,06 10-29 kg El = Dm c2 = 5,06 10-29 * 9 1016 = 4,55 10-12 J = 2,784 10-10/ 1,60 10-13 = 28,5 MeV. El /A = 28,5/4 = 7,1 MeV/nucléons. L'activité d'un gramme de radium est égale à A=3,7 1010 Bq = 1 curie. Temps de demi-vie t½ du radium : nombre de noyau de radium : N= 10-3 / m(22688Ra) = 10-3 / (225,9791*1,66606 10-27 ) = 2,656 1021 noyaux. constante radioactive l = A/N = 3,7 1010 / 2,656 1021 =1,393 10-11 s-1. t½ = ln2 / l =ln2 / 1,393 10-11 = 4,97 1010 s = 1,57 103 ans. Au bout de t½,50 % des noyaux de radium se sont désintégrés. Au bout de 2t½,75 % des noyaux de radium se sont désintégrés.
|
|||
|
|
|||
|
|