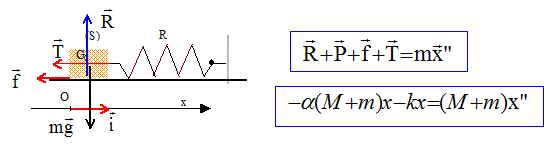|
Exercice
1 :
Deux petites boules ponctuelles sont suspendues au
même point A par un fil de longueur L, de masse
négligeable. Chaque boule possède une masse m
et porte la charge électrique q. A l'équilibre
les fils font un angle q
avec la verticale.
- Exprimer la tension T d'un fil
en fonction de L,q , sinq
et k = 1/(4pe0).
- On place en A une charge
électrique Q. Donner l'expression de Q pour que
l'équilibre précédent soit
conservé lorsqu'on coupe les fils.
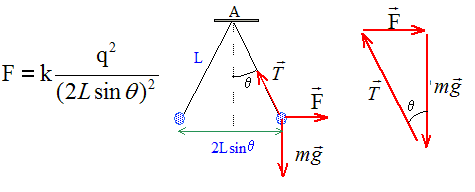
De plus sinq =
F/T soit T= F / sin q
; T= kq2 / (4L2
sin3q).
On place en A une charge
électrique Q. L'équilibre
précédent est conservé lorsqu'on coupe
les fils, si la force attractive, notée
F1, exercée par Q sur q est égale
à la tension. Les charges Q et q sont de signe
contraire.
F1=kQq/ L2 ;
T= kq2 /[(4L2
sin3q)
; kQq/ L2 = kq2
/ [(4L2 sin3q)
; Q = q / (4
sin3q).
Exercice
2 :
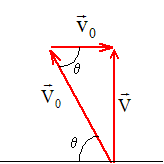
Un projectile est envoyé avec une vitesse
V0 dans une direction faisant un angle
q
avec le plan horizontal. L'engin qui tire le projectile se
déplace sur ce plan à la vitesse
v0.
- Comment doit être
orienté le tube lançant le projectile pour
que ce dernier parte à la verticale.
- Préciser la valeur de
q
lorsque V0 = 500 m/s et v0 = 15
m/s.
- Trouver la hauteur atteinte par
le projectile.
Référentiel terrestre
galiléen .
|
cosq
= v0/V0 =15/500 = 0,03
; q
=
88,3°.
V= [ V0
2-v02]½
= [
5002-152]½
= 499,77 m/s.
|
Hauteur atteinte par le projectile : H = V2/(2g)
= [ 5002-152] / 19,6
=1,27 104 m.
Exercice
6 :
Une source ultrasonore S émet une vibration
sinusoïdale à l'intérieur d'un tube
contenant de l'eau. La fréquence émise par S
est n0,
la célérité de l'onde dans l'eau est V.
La vibration issue de S provoque une variation de pression
Y=Acos(w0t+j)
en un point O tel que SO=l.
Quelle est la variation de pression en un point M d'abscisse
x>0 ?
--S------O-------M-------->
x
Au point M, on observe la variation
de pression produite en O avec un retard q=x/V
:
Y=Acos[w0(t-x/V)
+j].
Exercice
7 :
La masse de la terre est d'environ 5 1021 tonnes.
Montrer que, si la terre avait été
primitivement constituée uniquement de plutonium,
celui-ci aurait complétement disparu en 48 000
siècles, durée très inférieure
à l'âge de la terre. La période du
plutonium est 240 siècles. Masse d'une mole de
plutonium = 249 g.
48 000 siècles correspond
à : 48000/240 = 200 périodes.
A chaque période, le nombre
de noyaux initiaux ( donc la masse initiale ) de plutonium
est divisée par deux.
Au bout de 200 périodes, la
masse de plutonium restante est égale à la
masse initiale divisée par 2200 soit par :
1,6
1060.
Exercice
8 :
Un paquet d'ions monovalents est
accéléré à partir du repos par
un champ électrique de 3 104 V/m sur une
distance d=0,33 cm. A la sortie de ce champ, il parcourt 1
mm en 87 10-9 s.
- Déterminer la masse d'un de ces ions.
- Quel temps faudrait-il à un paquet de protons pour
parcourir 1 mm à la sortie du champ électrique
?
Le poids des ions est
négligeable devant la force électrique de
valeur F=eE.
La seconde loi de newton donne
l'accélération a = eE/m ;
La vitesse des ions à la
sortie du champ électrique vaut v2 = 2ad =
2eEd/m.
m =
2eEd/v2.
A la sortie de ce champ le
mouvement est rectiligne uniforme : vitesse v =
10-3/87 10-9=1,15 104
m/s
m= 2*1,6 10-19 * 3
104 *3,3 10-4/(1,15 104
)2=2,4
10-26
kg.
Temps mis par un paquet de
protons pour parcourir 1 mm à la sortie du champ
électrique
:
v2 = 2eEd/m= 2*1,6
10-19 * 3 104 *3,3 10-4 /
1,67 10-27 = 1,89 109 ; v = 4,36
104 m/s
Dt
= 10-3 / 4,36 104
=2,3 10-8
s.
Exercice
3 :
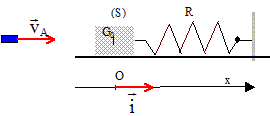
Un bloc de bois B de masse M, est placé sur un plan
horizontal. Un projectile A, de masse m, ayant une vitesse
vA horizontale, frappe ce bloc et s'y encastre.
Un ressort limite le déplacement de B. Avant le choc
le ressort n'a aucune déformation. Après le
choc, l'ensemble A+B se déplace en comprimant le
ressort dans la direction Ox. Le coefficient de raideur du
ressort est k.
- Le plan n'exerçant aucun
frottement, calculer la vitesse aquise par l'ensemble A+B
juste après le choc.
- Quel est en fonction du temps,
le déplacement x du système A+B glissant
sans frottement sur le plan ? Calculer la
fréquence, la période, l'amplitude du
mouvement.
- On suppose que le plan exerce
une force de frottement horizontale sur le système
glissant, opposée au mouvement. L'intensité
de cette force est proportionnelle au déplacement
x et à la masse m
du mobile f=amx.
Quel est alors le déplacement maximum de
l'ensemble A+B après impact du projectile ?
A.N : M=610 g ; m=30 g ; k=1,4 104 S.I ;
a=
6,55 104 S.I ; vA= 640
m/s.
Vitesse V aquise par
l'ensemble A+B juste après le choc :
La conservation de la quantité de mouvement
s'écrit : mvA = (M+m)V soit
V= m/(M+m) vA
= 0,03/0,64*640 = 30 m/s.
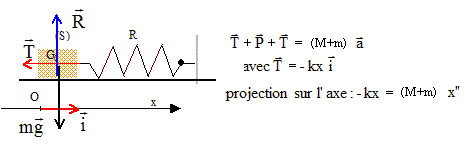
x"+k/(M+m) x=0 ; x"+w02x=0
avec w0 =[
k/(M+m)]½
=[1,4 104 /
(0,61+0,03)]½ =148 rad/s
fréquence : f = w0/
(2p) = 148 / (6,28)
= 23,55 Hz ;
période T=1/f = 4,2
10-2 s.
Conservation de l'énergie mécanique :
½(M+m)V2 = ½kA2 ;
A= V[(M+m)/k]½ =30*[0,64/1,4
104]½
=0,20 m.
Déplacement x du
système A+B : x(t) = 0,2
sin(148 t ).
On suppose que le plan exerce une
force de frottement horizontale sur le système
glissant, opposée au mouvement.
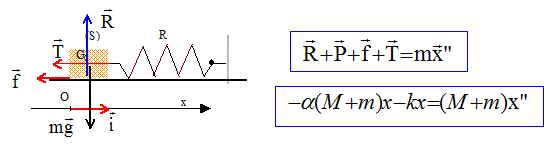
Dans l'expression de l'amplitude il suffit de
remplacer k par k1 = k+a(M+m)
= (1,4 + 6,55*0,64)104 = 5,59 104
S.I
Nouvelle amplitude A1 =
V[(M+m)/k1]½
=30*[0,64/5,59 104]½
=0,10 m.
Autre méthode : appliquer le
théorème de l'énergie
cinétique.
travail résistant de la tension
-½kA12 ;
travail résistant des frottements :
-½a(M+m)A12
;
variation de l'énergie cinétique :
0-½(M+m) V2.
|