Aurélie 23/05/07
 

concours électroradiologie médicale pendule simple. Nantes 2006

Google

 

Un pendule simple est constitué d'une bille de masse m, ponctuelle, attachée à l'extrémité d'un fil inextensible de longueur L, de masse négligeable. L'autre extrémité est attachée à un point O fixe. Ecarté de sa position d'équilibre le pendule oscille de part et d'autre de cette position d'équilibre.

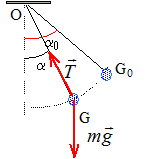
On repère la position du pendule par l'élongation angulaire a mesurée à partir de la position d'équilibre. L'intensité de la pesanteur est désignée par g.

 

  1. On considère un pendule écarté de sa position d'équilibre. En faisant le bilan des forces s'exerçant sur la bille et en utilisant une loi de la mécanique, que vous préciserez, montrer qu'une telle position ne peut pas être une position d'équilibre.
  2. Des élèves s'interrogent sur la période T des oscillations et sur la vitesse v de la bille au passage à la position d'équilibre. Les propositions sont les suivantes : k est un nombre sans dimension
    A. T=2p L/g ; B. T=2p ( L/g )½ ; C. T=2p L/(mg) ; g
    A' : v =kgL ; B' : v= k(gL)½ ; C' : k (mgL)½.
    Par analyse dimensionnelle déterminer les expressions qui peuvent convenir.
  3. Pour valider les résultats obtenus les élèves constituent 4 pendules différents. Les pendules sont écartés de am=5° de leur position d'équilibre et libérés sans vitesse. Les mouvements sont filmés et l'analyse des documents vidéo permet de trouver T et v. Les mesures sont regroupées dans le tableau suivant :
    n°1
    n°2
    n°3
    n°4
    m(g)
    100
    100
    200
    200
    L(cm)
    25
    50
    25
    50
    T(s)
    1,00
    1,42
    1,00
    1,42
    v(m/s)
    0,14
    0,19
    0,14
    0,19
    Etude de la période :

    - Montrer que les mesures permettent d'éliminer la relation C.
    - Montrer que la relation A ne peut pas convenir.
    - Trouver une valeur de l'intensité de la pesanteur avec les données fournies.
    Etude de la vitesse au passage à la position d'équilibre.
    Quelles relations peuvent être éliminées et pourquoi ? On donne     p2=9,87.

On considère un pendule écarté de sa position d'équilibre.

La somme vectorielle du poids et de la tension du fil n'est pas nulle.

D'après la première loi de Newton ( ou principe d'inertie) dans cette position la valeur de la vitesse, initialement nulle, va changer et la bille va se déplacer ; cette position ne peut être une position d'équilibre.

Analyse dimensionnelle :

2p et k sont sans dimensions ;

L : longueur ; g : accélération soit une longueur / temps2; m est une masse.
2p L/g : temps2 ; [2p L/g ]= T2 : A ne convient pas.

[2p ( L/g )½ ] = T : B convient.

2p L/(mg) : longueur / ( masse * accélération) ; temps2/masse ; [2p L/(mg)]= T2 M-1 : C ne convient pas.

gL ; accélération * longueur ; longueur2/temps2 ; [kgL]= L2T-2 : A' ne convient pas.

[ k(gL)½]=L T-1 : B' convient.

[ k (mgL)½]= M-1L T-1 : C' ne convient pas.

n°1
n°2
n°3
n°4
m(g)
100
100
200
200
L(cm)
25
50
25
50
T(s)
1,00
1,42
1,00
1,42
v(m/s)
0,14
0,19
0,14
0,19
Etude de la période :

Les mesures indiquent que la période est indépendante de la masse ( pendules n°1 et n°3 par exemple) :

la relation C dans laquelle figure la masse, ne peut pas convenir.

Les mesures indiquent que la période n'est pas proportionnelle à la longueur ( pendule n°1 et n°2 par exemple).

la relation A dans laquelle T et L sont proportionnels, ne peut pas convenir.
Valeur de l'intensité de la pesanteur ( pendule n°1) :

[2p ( L/g )½ ] = T ; g= 4p2 L/T2=4*9,87*0,25 = 9,87 m/s2.

 

Etude de la vitesse au passage à la position d'équilibre.

Les mesures indiquent que la vitesse maximale est indépendante de la masse ( pendule n°1 et n°3 par exemple).

La relation C' est donc éliminée car elle fait intervenir la masse.
Les mesures indiquent que la vitesse maximale n'est pas proportionnelle à la longueur ( pendule n°1 et n°2 par exemple).

La relation A' est donc éliminée.

 

retour -menu