Aurélie 23/05/07
 

concours électroradiologie médicale dipoles RC et LC. Nantes 2006

Google

 

A. Etude d'un condensateur :

  1. Un générateur idéal de tension constante notée E alimente un condensateur de capacité C en série avec un conducteur ohmique R.

    Le condensateur est initialement déchargé et on souhaite visualiser à l'aide d'un oscilloscope à mémoire, la tension uD aux bornes du dipole "RC" ( voie A) et la tension uC ( voie B) aux bornes du condensateur, lors de la fermeture du circuit. les branchements sont indiqués sur la figure.
    - Compléter ce schéma en représentant les flèches des tensions visualisées sur chaque voie.

  2. On ferme l'interrupteur et on enregistre les tensions. L'écran de l'oscilloscope est représenté ci-dessous : ( 2V/div et 0,5 ms/div).

    A quelle voie de l'oscilloscope correspond chaque courbe ? Justifier.

  3. Etablir la relation entre la tension E et les tensions uR aux bornes du conducteur ohmique et uC aux bornes du condensateur.
    - Déterminer l'équation différentielle vérifiée par uC pendant la charge.
    - La solution de cette équation est de la forme uC(t) = A +B exp(-t/    t). Déterminer A et Bet en déduire l'expression de uC(t).
  4. Déterminer à l'aide de l'oscillogramme la valeur de E.
  5. La constante de temps est t = RC. Montrer par analyse dimensionnelle que t a la dimension d'un temps.
    - Déterminer graphiquement     t et expliquer la méthode utilisée.
    - Si C= 1     mF calculer la valeur de R.
B. Association condensateur bobine.

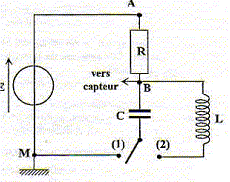
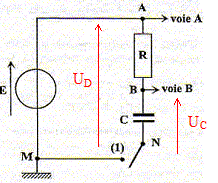
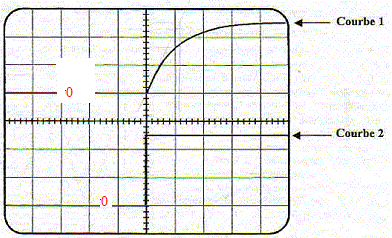
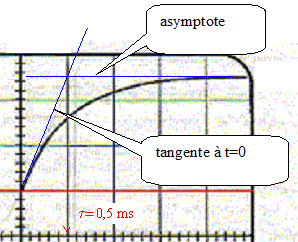
On associe le condensateur chargé sous une tension de 5 V à une bobine d'inductance L et de résistance négligeable. Un ordinateur + carte d'acquisition permet de visualiser la tension uc(t) aux bornes du condensateur. Le début de l'enregistrement (t=0) est synchronisé avec la fermeture de l'interrupteur en position 2. La courbe obtenue est donnée ci-dessous : ( 2 V/div ; 1 ms/div)

 

  1. Comment caractérise t-on le phénomène observé ?
  2. La période est donnée par l'expression T0 = 2p(LC)½.
    - Calculer la période et en déduire la valeur de l'inductance.
  3. Le plus souvent la bobine possède une résistance. Comment le graphique précédent aurait il été modifié ? Comment qualifierait-on le régime observé ?
    0,63*2,5 = 1,6 ;     p2 = 10.
 

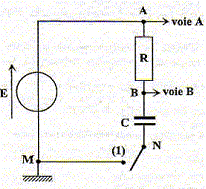
La tension aux bornes du condensateur en charge à travers un résistor est croissante de 0 à E= 5 V : courbe 1( voie B).

La tension aux bornes du dipole "RC" est constante, égale à E =5 V: courbe 2 ( voie A)

Relation entre la tension E et les tensions uR aux bornes du conducteur ohmique et uC aux bornes du condensateur.

E= uR+uC, additivité des tensions.
Equation différentielle vérifiée par uC pendant la charge .

E= uR+uC avec uR= R i ; i = dq/dt et q= CuC d'où i = C duC/dt.

E= RC duC/dt + uC.
La solution de cette équation est de la forme uC(t) = A +B exp(-t/t).

Déterminons A et B :

A l'instant initial t=0, le condensateur n'est pas chargé et uC(0)=0 = A+ B.

A un instant suffisamment long, le condensateur est chargé et uC(oo) = E= A ; par suite B= -E.

uC(t) = E(1- exp(-t/t)).

La constante de temps est t = RC.

Montrons par analyse dimensionnelle que t a la dimension d'un temps.

R : tension / intensité ; C : charge / tension soit intensité * temps / tension

par suite RC a la dimension d'un temps.

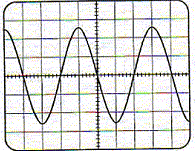
Si C= 1 mF la valeur de R est : R= t/C =5 10-4 / 10-6 = 500 W.

B. Association condensateur bobine.

Le phénomène observé :

L'échange permanent d'énergie entre condensateur et bobine conduit à l'observation d'une tension sinusoïdale périodique aux bornes du condensateur.

La période est donnée par l'expression T0 = 2p(LC)½.
D'après le graphe, une période correspond à 4 divisions soit à 4 ms ; T0 = 4 10-3 s.

Inductance L :

L= T02/(4p2C) = 16 10-6/(4*10 *10-6) ; L= 0,4 H.

Le plus souvent la bobine possède une résistance.

Sur le graphique précédent on observerait une diminution de l'amplitude des oscillations.

Le régime est alors pseudopériodique.

 

retour -menu