|
|
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
Un générateur maintient entre ces bornes A et B une tension sinusoïdale d'amplitude Umax=325,26 V et de fréquence f = 50 Hz. On branche en série aux bornes de A et B un condensateur de capacité C= 200 mF et une bobine d'inductance L= 0,29 H et de résistance interne R= 30 W.
corrigé 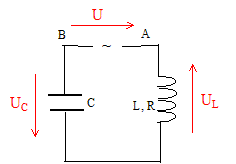
Valeur efficace de la tension du générateur : Ueff = Umax / 2½ = 325,26 / 2½ =230 V Impédance Z du circuit : Z = [R2 + (Lw-1/(Cw))2]½. w = 2*3,14 *50 = 314 rad/s ; Lw = 0,29*314 = 91 W ; 1/(Cw) = 1/(2 10-4 *314) =15,9 W ; Z= [302 +
(91-15,9)2]½ = 80,9
W.
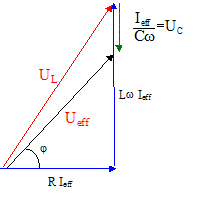
intensité efficace : Ieff = Ueff / Z = 230/80 = 2,87 A. Tension efficace UC aux bornes du condensateur : UC = Ieff / (Cw) = 2,87*15,9 = 45,7 V. Tension efficace UL aux bornes de la bobine :
UL=[R2+(Lw)2]½Ieff =[900+912]½ *2,87 =275 V. Angle de déphasage j du circuit : tan j = (Lw-1/(Cw)) / R = (91-15,9) / 30 = 2,5 ; j = 68°.
|
|||||||||||||||||||||||||||||||||||
|
corrigé La pression diminue lorsque l'altitude augmente. Les unités de pressions les plus couramment utilisées : bar ; pascal ( Pa) ; hPa 1 bar = 105Pa ; 1 torr = 1 mm Hg et 760 mmHg correspondent à 105 Pa soit 1 torr = 1 mmHg = 105/760 = 132 Pa 1 mbar = 100 Pa = 100/132 mmHg = 0,76 mmHg ; 1 mmHg =1,32 mbar. Quelques appareils de mesures de pression :
manomètre, baromètre ( mesure de la pression
atmosphérique), vacuomètre ( mesure du vide
résiduel)
Force (N) = pression ( Pa) * surface (m2) Force exercée par l'air extérieur, dirigée vers l'intérieur de l'enceinte, valeur : Fext =105*2,54 10-2 =2,54 103 N Force exercée par l'air intérieur, dirigée vers l'extérieur de l'enceinte, valeur : Fint =10-2*2,54 10-2 =2,54 10-4 N Force résultante, dirigée vers l'intérieur de l'enceinte, valeur : F=2,54 103 N |
|||||||||||||||||||||||||||||||||||
corrigé 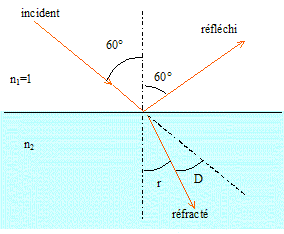
Le milieu (1) est l'air, le milieu (2) est un verre : D= 60-r d'où r = 60-D = 60-30 = 30° loi de Descartes : n1 sin 60 = n2 sin r ; n2 = n1 sin 60 / sin r = sin 60 / sin 30 = 1,73. Le milieu (1) est le verre précédent et le milieu (2) est de l'air ; l'angle d'incidence vaut encore 60 °. Le faisceau réfracté existe si l'angle d'incidence est inférieure à imax tel que sin imax = 1/n2 ; sin imax = 1/1,73 =0,577 soit imax =35°. Or l'angle d'incidence vaut 60°, valeur supérieure à imax : il y a réflexion totale. 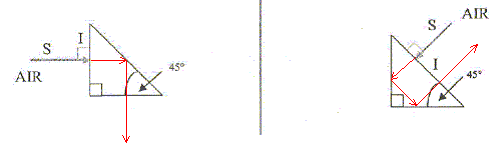
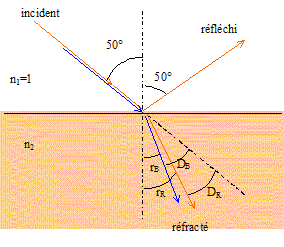
D'une part, un faisceau perpendiculaire à la surface séparant deux milieux transparents, n'est pas dévié. D'autre part, le faisceau réfracté existe si l'angle d'incidence est inférieure à imax tel que sin imax = 1/n2 ; sin imax = 1/1,50 =0,667 soit imax =42°. Or l'angle d'incidence vaut 45°, valeur supérieure à imax : il y a réflexion totale. Un pinceau de lumière blanche arrive sous l'angle d'incidence i = 50° à la surface de séparation plane de l'air et du verre. indice de réfraction du verre pour le bleu nB= 1,524 ; pour le rouge nR = 1,515.
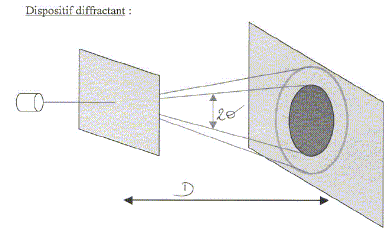
D'une part, pour le faisceau bleu : sin 50 = nB sin rB soit sin rB = sin 50 / nB = sin 50 / 1,524 =0,5026 ; rB =30,17° ; DB=50-30,17 = 19,83° D'autre part, pour le faisceau rouge : sin 50 = nR sin rR soit sin rR = sin 50 / nR = sin 50 / 1,515 =0,5056 ; rR =30,37° ; DR=50-30,37 = 19,63° Valeur de l'angle entre deux rayons, un bleu et un rouge, transmis par le verre : 30,37-30,17 = 0,2°. Le rayon bleu subit la plus grande déviation. Calcul les rayons des premiers maxima et minima de lumière sachant que l'angle q est donné par les formules :
|
|||||||||||||||||||||||||||||||||||
corrigé Les équivalences : T(K) = q(°C) +273 ; 1K= 1°C. unité de R : R= PV/(nT) PV : pression * volume ( Pa m3) ; or une pression est une force (N) / surface(m2) d'où PV a la dimension d'une force* longueur, soit une énergie ( J) n : mol ; T : K ; par suite R a la dimension suivante : J
mol-1 K-1.
Lq = L0(1+a(273+q)) Lq1 = L0(1+a(273+q1)) ; Lq2 = L0(1+a(273+q2)) ; DL = Lq2 -Lq1 =L0a[q2-q1] DL
=100*12 10-6 (50+20) = 0,084 m =
8,4
cm.
Energie Qc cédée par le corps chaud, l'aluminium : Qc =maca(q éq-q a) Energie Qf gagnée par les corps froids, l'eau et le calorimètre : Qf =(me+m)ce(q éq-q e) système adiabatique, sans échange de chaleur avec l'extérieur : Qc + Qf = 0 maca(q éq-q a) + (me+m)ce(q éq-q e) =0 ca = (me+m)ce(q éq-q e) / [ma(q a-q éq) ] ca = 0,24*4185*(33-21,1) / (0,199*67)= 896 J kg-1 K-1.
|
|||||||||||||||||||||||||||||||||||
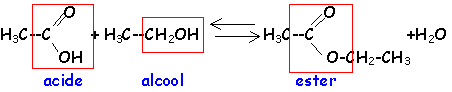
corrigé réaction d'un acide organique sur un alcool : estérification
Pour préparer une solution d'acide sulfurique, il faut ajouter l'acide dans l'eau. Le pHmètre mesure l'acidité d'une solution. 4Al + 3MnO2 --> 2Al2O3 + 3Mn. propane : CH3-CH2-CH3 ;
1,2-dibromoéthane : BrCH2-CH2Br
; benzène : Signification des pictogrammes :
1 : danger électrique ; 2 : extincteur ; 3 : interdit aux véhicules de manutention ; 4 : risque d'explosion 5 : douche de sécurité ; 6 : téléphone pour premiers secours ; 7 : défense d'éteindre avec de l'eau ; 8 : port du casque obligatoire.
|
|||||||||||||||||||||||||||||||||||
corrigé Potentiel du point E+, entrée non inverseuse : E+ = V2/R3 / [1/R3+1/R4] Potentiel du point E-, entrée inverseuse : E- = [V1/R1 +V0/R2] / [1/R1+1/R2] Or E+ =E- ;V2/R3 [1/R1+1/R2] =[V1/R1 +V0/R2] [1/R3+1/R4] Or R1 = R3 et R2 = R4 : V2/R1 [1/R1+1/R2] =[V1/R1 +V0/R2] [1/R1+1/R2] V2/R1=V1/R1 +V0/R2 ; (V2-V1)/R1=V0/R2 ; V0 =R2/R1(V2-V1) Ce montage réalise une amplification et une soustraction. V0 =R2/R1(V2-V1) = 4,7/3,3 = 1,42 V. |
|||||||||||||||||||||||||||||||||||
|
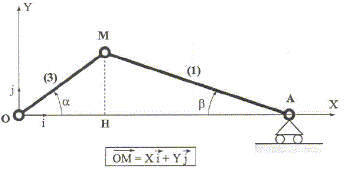
Un système mécanique constitué d'un vilbrequin peut être représenté sous la forme suivante : le point O est le centre de rotation du vilbrequin, les points A et M sont les extrémités de la bielle, H est le projeté de M sur l'axe i. OM= 20 mm et MA= 100 mm
corrigé Le point A est animé d'un mouvement rectiligne sur l'axe Ox. X= OM cos a et Y= OM sin a Expression de sin b en fonction de OM, AM et sin a : triangle OMH : MH= OM sin a ; triangle AMH : MH= AM sin b ; sin b=OM sin a /AM = 1/5 sin a= 0,2 sin a. Expression du bipoint OA : OH + HA OH = OM cos a ; AH=MA cos b ; OH + HA = OM cos a +MA cos b = OM[ cos a +MA/OM cos b ] or MA/OM = 5 : OH + HA =OM[ cos a +5 cos b ] cos b = (1-sin2b)½ : OH + HA =OM[ cos a +5 (1-sin2b)½ ] sin b=0,2 sin a : OH + HA =OM[ cos a +5 (1-0,04sin2a)½ ] sin2a = 1 - cos2a : OH + HA =OM[ cos a +5 (1-0,04+ 0,04cos2a)½ ] OH + HA =OM[ cos a + (0,96*25+ 0,04*25cos2a)½ ] =OM[ cos a + (24+ cos2a)½ ] |
|||||||||||||||||||||||||||||||||||
|
|