Aurélie 2/05/07
 

Concours kiné Limoges : radioactivité et scintigraphie ; dipole RL 2007

Google

 

Radioactivité et scintigraphie ( 4 pts)

La scintigraphie est une technique d'investigation médicale qui permet l'observation de la glande thyroïde.

Un patient insère pour cette observation une masse m=1,31 ng de l'isotope13153I de l'iode qui est radioactif de type b-.

  1. Ecrire l'équation de la réaction de désintégration en justifiant.
  2. Déterminer le nombre d'atomes radioactifs dans la dose ingérée.
  3. On note N0 le nombre de noyaux radioactifs à la date t=0. On note N le nombre de niyaux radioactifs à la date t.
    Etablir la relation entre la constante radioactive     l et le temps de demi-vie t½, en précisant la signification de la demi-vie.
  4. Définir l'activité d'un échantillon radioactif et établir la relation entre l'activité et N.
  5. Calculer l'activité initiale de la dose ingérée.
  6. Calculer le temps au bout duquel l'activité résiduelle est égale à 1,5 % de l'activité initiale.
Données : masse molaire de l'iode 131 : M voisin 131 g/mol ; NA voisine 6 1023 mol-1 ; t½ de l'iode 131= 8,1 jours = 7 105 s ;

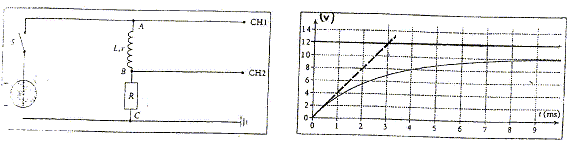
ln2/7 = 0,1 ; ln 0,015 = -4,2 ; 4,2 / ln2 = 6.

51Sb ; 52Te ; 54Xe ; 55Cs ; 56Ba.

Etablissement d'un courant dans un dipole RL (5 pts)

 Une bobine d'inductance L et de résistance r est mise en série avec un conducteur ohmique de résistance R= 40 W. Un interrupteur S permet de connecter l'ensemble à un générateur de tension de fem E= 12,0 V. Les points A et B sont respectivement reliés aux entrées CH1 et CH2 d'un oscilloscope à mémoire, le point C étant relié à la masse.

A la fermeture de l'interrupteurS, on a enregistré les tensions aux entrées CH1 et CH2, puis on a fait trracer en pointillés la tangente à la courbe exponentielle à la date t=0.

  1. Quelle tension est visualisée sur CH1 ? Quelle est sa valeur ?
  2. Quelle tension est visualisée sur CH2 ? Comment peut-on en déduire l'intensité du courant traversant le circuit ?
  3. Quelle est la valeur de l'intensité du courant en régime permanent ?
    - Quelle est la valeur de la dérivée de l'intensité du courant par rapport au temps à t=0 ?
  4. Etablir l'équation différentielle à laquelle obéit l'intensité du courant traversant le circuit.
  5. Utiliser l'équation précédente :
    Lorsque le régime permanent est établi pour trouver la résistance r de la bobine.
    - à t=0 pour trouver son inductance L.
  6. La solution de l'équation différentielle est de la forme i= A(1-exp(-t/t).
    Etablir les expressions de A et de t.
  7. Utiliser la courbe pout trouver la valeur de la constante de temps du circuit. Justifier.
    Comparer avec le résultat obtenu à la question précédente.
Radioactivité et scintigraphie ( 4 pts)

Un patient insère pour cette observation une masse m=1,31 ng de l'isotope13153I de l'iode qui est radioactif de type b-.

Equation de la réaction de désintégration :

13153I --->AZX +0-1e.

conservation du nombre de nucléons : 131 = A

conservation de la charge : 53=Z-1 d'où Z= 54

On identifie AZX à 13154Xe.

Nombre d'atomes radioactifs dans la dose ingérée :

n= m/M = 1,31 10-9 / 131 = 10-11 mol.

N0 = nNA = 10-11*6 1023 = 6 1012 noyaux.

Relation entre la constante radioactive l et le temps de demi-vie t½ :

On note N0 le nombre de noyaux radioactifs à la date t=0. On note N le nombre de niyaux radioactifs à la date t.
t½ : durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.
N(t) =N0 exp(-lt) loi de décroissance radioactive

N(t½) =½N0 =N0 exp(-lt½) ; ln0,5 = -lt½

lt½ = ln2.

Activité d'un échantillon radioactif :

A : nombre moyen de désintégrations par seconde

A= -dN/dt avec N= N(t) =N0 exp(-lt) ; dN/dt = N0(-l)exp(-lt)

A = l N.

Activité initiale de la dose ingérée : A0 = l N0.

l = ln2 /t½= ln2 /(7 105 )=0,1 *10-5 = 10-6 s-1.

A0 =10-6* 6 1012 ; A0 = 6 106 Bq.

Temps au bout duquel l'activité résiduelle est égale à 1,5 % de l'activité initiale :

A(t) = A0 exp(-lt) avec A(t) = 0,015 A0.

0,015 = exp(-lt) ; ln 0,015 = -lt ; 4,2 = lt ; t = 4,2 / l ; t = 4,2 / 10-6 ; t = 4,2 106 s.

 

 Etablissement d'un courant dans un dipole RL (5 pts)

 Une bobine d'inductance L et de résistance r est mise en série avec un conducteur ohmique de résistance R= 40 W. Un interrupteur S permet de connecter l'ensemble à un générateur de tension de fem E= 12,0 V. Les points A et B sont respectivement reliés aux entrées CH1 et CH2 d'un oscilloscope à mémoire, le point C étant relié à la masse.

A la fermeture de l'interrupteurS, on a enregistré les tensions aux entrées CH1 et CH2, puis on a fait trracer en pointillés la tangente à la courbe exponentielle à la date t=0.

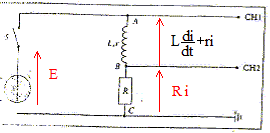
Sur CH1 on visualise la tension uAC = E =12,0 V.( aux bornes du générateur de tension).

Sur CH2 on visualise la tension uBC = R i(t) ; uBC est l'image de l'intensité au facteur R près :

i(t) = uBC/ R.

Valeur de l'intensité du courant en régime permanent :

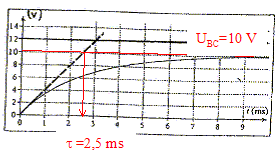
I = 10/R = 10/40 = 0,25 A.
Valeur de la dérivée de l'intensité du courant par rapport au temps à t=0 :

Coefficient directeur de la tangente à la courbe ci-dessus à t=0 : [dUBC/dt]t=0 = 10 /2,5 10-3 = 4 103 V s-1.

or uBC = R i(t) d'où : [dUBC/dt] = R [di/dt]

[di/dt]t=0 =1/R [dUBC/dt]t=0 =4000 / 40 ; [di/dt]t=0 = 100 A s-1.

Equation différentielle à laquelle obéit l'intensité du courant traversant le circuit :

E = Ri + Ldi/dt + ri

E= (R+r)i + Ldi/dt

di/dt +(R+r)/L i = E/L.

Lorsque le régime permanent est établi : di/dt = 0 soit (R+r) I= E

R+r = E/I ; r = E/I -R ; r = 12/0,25 -40 ; r = 8 W.

à t=0 , [di/dt]t=0 =100 A s-1 ; [di/dt]t=0 =E/L ;

L = E / [di/dt]t=0 = 12/100 ; L= 0,12 H.

La solution de l'équation différentielle est de la forme i= A(1-exp(-t/t).
Expressions de A et de t :

di/dt = A t exp(-t/t)

Repport dans l'équation différentielle :

A t exp(-t/t)+(R+r)/L A(1-exp(-t/t) = E/L

égalité vérifiée quel que soit t si : A = E/(R+r) = intensité en régime permanent

et si : t = L/(R+r) ; t = 0,12 /(40+8) = 2,5 10-3 s = 2,5 ms ( en accord avec la valeur lue sur le graphe).
 

retour -menu