Concours kiné Limoges : mouvement d'un skieur ; datation au carbone 14 2007

Les vecteurs sont écrits en gras et en bleu.

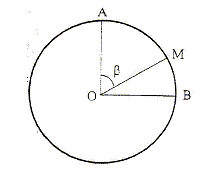
On assimile le skieur à un point matériel et la trajectoire est dans un plan vertical.

Le skieur aborde avec une vitesse quasi-nulle la piste AB constituée par un quart de cercle de rayon r. La piste est verglassée et les frottements sont négligeables. Il perd le contact avec la piste en M.

Données : carbone 12 ¹²₆C ; carbone 13 ¹³₆C ; azote 14 ¹⁴₇N ; ln2 = 0,6 ; ln3=1,0

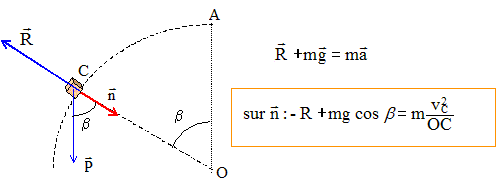
Le skieur est soumis à son poids et à l'action du support :

En M, le skieur perd le contact avec le plan ( R=0) d'où : v²_M = r g cos b

v_M = [r g cosb]^½.

Théorème de l'énergie cinétique entre A et M :

Travail moteur ( descente) du poids : mg r(1-cos b )

R, perpendiculaire à la vitesse ne travaille pas.

½m v²_M -0 = mg r(1-cos b )

or v²_M = r g cos b d'où : ½m r g cos b= mg r(1-cos b )

1,5 cosb = 1 ; cos b = 1/1,5 ; cos b =2/3.

Valeur de la vitesse en M :

r= 3,6 m ; g = 10 m/s² ; (2/3)^½ = 0,8 ; (3/2)^½ = 1,2.

v_M = [3,6*10 *2/3]^½ = 6*0,8 ; v_M =4,8 m/s.

 Datation au carbone 14 :

Données : carbone 12 ¹²₆C ; carbone 13 ¹³₆C ; azote 14 ¹⁴₇N ; ln2 = 0,6 ; ln3=1,0

Le bombardement des noyaux d'azote dans la haute atmosphère par les neutrons aboutit à la réaction nucléaire dont l'équation est la suivante :

¹⁴₇N +¹₀n = ^A_ZY₁ + ¹₁H (1)

Lois de conservation permettant d'écrire l'équation:

Conservation de la charge : 7+0 = Z+1 d'où Z= 6 et Y₁ est l'élément carbone.

conservation du nombre de nucléons : 14+1=A+1 d'où A=14

^A_ZY₁ est identifié à ¹⁴₆C

La désintégration du noyau de carbone 14 conduit à l'émission d'un électron de symbole ⁰_-1e et d'un noyau ^A_ZY₂.
Equation de la réaction nucléaire correspondante :

¹⁴₆C --> ⁰_-1e + ^A_ZY₂ ; radioactivité de type b^-.

Conservation de la charge : 6 = Z-1 d'où Z= 7 et Y₂ est l'élément azote.

conservation du nombre de nucléons : 14=A

^A_ZY₇ est identifié à ¹⁴₇N

Le temps de demi-vie du carbone 14 noté t_½ est de l'ordre de 6000 ans.
Définition du temps de demi-vie :

Durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.
l t_½ = ln2 ; l s'exprime en s^-1 ou an^-1 ( inverse d'un temps).

A la fin du XX^ème siècle, les vestiges d'une fresque peinte furent découverte à Thèbes, anciennement Louxor, capitale d'Egypte. Une datation au carbone 14 est réalisée sur un échantillon de cette fresque. L'activité de cet échantillon est de 10,0 désintégrations par minute et par gramme de carbone. Or l'activité pour 1 g de carbone participant au cycle du dioxyde de carbone atmosphérique est estimée à 15,0 désintégrations par minute.

Année approximative de la réalisation de la fresque :

A(t) = A₀ exp(-lt) ; ln (A₀/ A(t) ) = lt = ln2 t/t_½.

On pose t/t_½ = n ; ln (A₀/ A(t) ) = n ln2 = ln 2ⁿ.

A₀/ A(t) = 2ⁿ ; 15/10 = 2ⁿ ; ln 1,5 = n ln2 ; n= ln1,5/ ln2

n = ln(3/2) / ln2 = (ln3-ln2)/ln2 = (1-0,6) / 0,6 = 4/6 = 2/3.

t = n t½ = 2/3*6000 = 4000 ans.