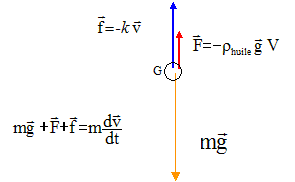Aurélie 2/05/07
 

Concours kiné Limoges : viscosité d'une huile moteur : Euler 2007

Google

 

Les vecteurs sont écrits en gras et en bleu.

On filme la chute verticale d'une bille dans une huile moteur avec une caméra numérique. On désignera par m la masse de la bille, par R son rayon et par V son volume. On appellera rhuile la masse volumique de l'huile.

  1. Pour étudier le mouvement de la bille, on se place dans le référentiel du laboratoire. On prendra l'axe vertical z'z dirigé vers le bas. On suppose que la force de frottement s'exprime sous la forme f= -kv où v est le vecteur vitesse du centre d'inertie de la bille.
    - Faire l'inventaire des forces appliquées à la bille puis les représenter sur un schéma.
  2. En appliquant la deuxième loi de Newton, établir l'équation différentielle du mouvement de la bille.
  3. dv/dt peut se mettre sous la forme dv/dt = A-Bv. Exprimer les constantes A et B en fonction des données.
  4. Dans le système internationnal A= 1,00 et B= 10,0. Préciser leurs unités.
  5. Quelle est la valeur de la vitesse limite vl ?
  6. La méthode d'Euler permet d'estimer par le calcul la valeur de la vitesse de la bille en fonction du temps. On obtient :
    t(s)
    0
    0,010
    0,020
    0,030
    0,040
    v(m/s)
    0
    ?
    ?
    0,027
    0,034
    - Quel est le pas d'itération de la méthode ?
    - Calculer les valeurs v1 et v2 de la vitesse à t = 0,010 et t = 0,020 s.
    - Comment améliorer la résolution de l'équation différentielle par la méthode d'Euler ?
  7. Pour les vitesses faibles, la formule de Stokes donne la relation entre la force de frottement f agissant sur la bille de rayon R, la vitesse V et la viscosité h de l'huile : f = -6phRv avec h en Pa s, R en m et v en m/s.
    - En vous aidant de l'expression de B et de l'hypothèse     f=-kv, exprimer la viscosité h en fonction de B, m et R.
    - Calculer la viscosité (     p =3, m=1,8 g et R= 2 mm)
    Identifier l'huile moteur utilisée.
    huile moteur à 20°C

    SAE10
    SAE30
    SAE50
    h( Pa s)
    0,088
    0,290
    0,500
 

Inventaire des forces appliquées à la bille :

- Poids, verticale, vers le bas, valeur P=mg

- Poussée d'Archimède, verticale, vers le haut , valeur F= V rhuileg

- Force de foottement , verticale, vers le haut, valeur f=kv.

Equation différentielle du mouvement de la bille :

Ecrire la deuxième loi de Newton sur un axe vertical, orienté vers le bas :

mg -V rhuileg-kv = mdv/dt

dv/dt = g(1-V rhuile/m)-k/m v.

A= g(1-V rhuile/m) et B =k/m.

dv/dt = A-Bv ; A a la dimension d'une accélération ( m s-2).

B a la dimension d'une accélération divisée par une vitesse : B s'exprime en s-1.

Valeur de la vitesse limite vl :

dvl/dt = 0 soit A-Bvl=0 ; vl = A/B = 1,00/10,0 ; vl = 0,100 m/s.

La méthode d'Euler permet d'estimer par le calcul la valeur de la vitesse de la bille en fonction du temps. On obtient :
t(s)
0
0,010
0,020
0,030
0,040
v(m/s)
0
?
?
0,027
0,034
Pas d'itération de la méthode : Dt= 0,01 s.
Valeurs v1 à t = 0,010 :

Dv/Dt = A+B v(t) et Dv = v(t+Dt) - v(t) ; v(t+Dt) = v(t) +Dv

[Dv/Dt]t=0 =A-Bv(0) = A = 1 m/s² ; Dv=ADt =1*0,01=0,01m/s

v1 = v(0) +Dv = 0+0,01 ; v1 = 0,01 m/s.

[Dv/Dt]t=0,01 =A-Bv(0,01) = 1- 10*0,01 =0,9 m/s² ; Dv=0,9Dt =0,9*0,01=0,009m/s

v2 = v1 +Dv = 0,01+0,009 ; v2 = 0,019 m/s.

On améliore la résolution de l'équation différentielle par la méthode d'Euler en prenant un pas plus petit.

Pour les vitesses faibles, la formule de Stokes donne la relation entre la force de frottement f agissant sur la bille de rayon R, la vitesse V et la viscosité h de l'huile : f = -6phRv avec h en Pa s, R en m et v en m/s.

de plus f=-kv et B = k/m
Exprimer la viscosité h en fonction de B, m et R :

k = 6phR ; B= 6phR / m ; h = Bm /(6pR).
Si p =3, m=1,8 g et R= 2 mm :

h = 10*1,8 10-3/(6*3*2 10-3) ; h =0,500 Pa s.
L'huile moteur utiliséeest SAE 50.

 

 
 

retour -menu