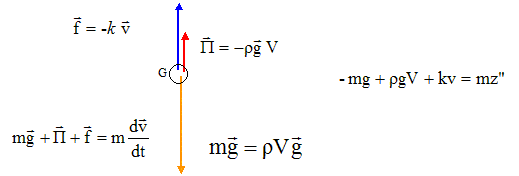|
concours Geipi Eni
chute dans l'eau,
radioactivité, dipoles LC, RC.
2007
|
|||
|
|||
|
Cette bille de volume V est freinée par la viscosite de l'eau. La norme de cette force de frottement vaut : f=k v avec v la norme de la vitesse de la bille. Quelle est l'équation de son mouvement, en prenant l'axe (Oz) vertical et ascendant ? La bille est soumise à son poids, à la poussée d'Archimède et à la force de frottements :
A. mz" = mg +rgV-kv. Faux. B. mz" = - mg -rgV+kv. Faux. C. mz" = -mg +rgV+kv. Vrai. D. mz" = -mg +rgV-kv. Faux. E. mz" = mg -rgV+kv. Faux.
Cet élément radioactif produit des noyaux d’yttrium 9039Y. La durée de demi vie du strontium est de 29 ans. Quelle est la nature de la radioactivité ? 9038Sr -->9039Y +AZX conservation du nombre de nucléons : 90 =90 +A d'où A=0 conservation de la charge : 38 = 39 +Z d'où Z=-1 AZX est identifié à un électron 0-1e A. a. Faux. B. b-. Vrai. C. b+. Faux. D. g. Faux. E. fission. Faux. En 2007, on utilise un capteur Geiger dont la fenêtre d’entrée a une surface de 50 mm2. On place cette fenêtre du capteur à 10 cm en face d’une source de strontium 9038Sr Ce capteur ne mesure qu’une fraction de l’activité de la source. Il indique 100 Bq. On retrouve dans une armoire un ancien compte rendu d’expérience effectuée avec la même source. Le capteur de l’époque possédait une fenêtre d’entrée de surface 100 mm2. Lorsque la source était placée à 10 cm du capteur, celui-ci indiquait 400 Bq. En quelle année ce compte rendu a-t-il été écrit ? L'activité serait 200 Bq pour une fenêtre d'entrée de 50 mm2. L'activité a été divisée par 2 : la durée est donc égale à une demi-vie soit 29 ans d'où 2007-29 = 1978. A. 2006. Faux. B. 1978. Vrai. C. 1949. Faux. D. 1920. Faux. E. 1891. Faux.
Un condensateur, de charge initiale Q0, est déchargé à travers une résistance R. La constante de temps caractéristique de charge et décharge de ce condensateur, associé à la résistance R, est notée t. On rappelle que la tension aux bornes du condensateur durant la décharge est de la forme : uC = a+ b exp (-t /t) Au bout de combien de temps la charge du condensateur a-t-elle été divisée par 2 ? La charge et la tension aux bornes du condensateur sont proportionnelles. Q0 = CuC(0) CuC(0) = a+ b =Q0. Au bout d'un temps suffisamment grand la charge est nulle : 0 = a ; b =Q0. uC =Q0/C exp (-t /t). ½uC(0) =½Q0/C= Q0/C exp (-t /t) ; 0,5 = exp (-t /t) ; ln 0,5 = -t /t ; ln2 = t /t ; t=t ln2. A. t. Faux. B. t ln2. Vrai. C. t/e. Faux. D. t/2. Faux. E. ln2/t . Faux.
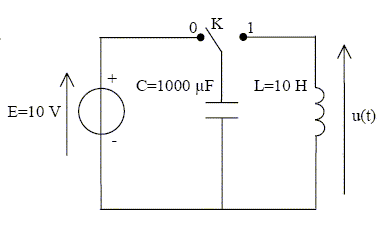
Initialement K était en 0 depuis un temps très long. A t =0 , on bascule l’interrupteur K de 0 vers 1.
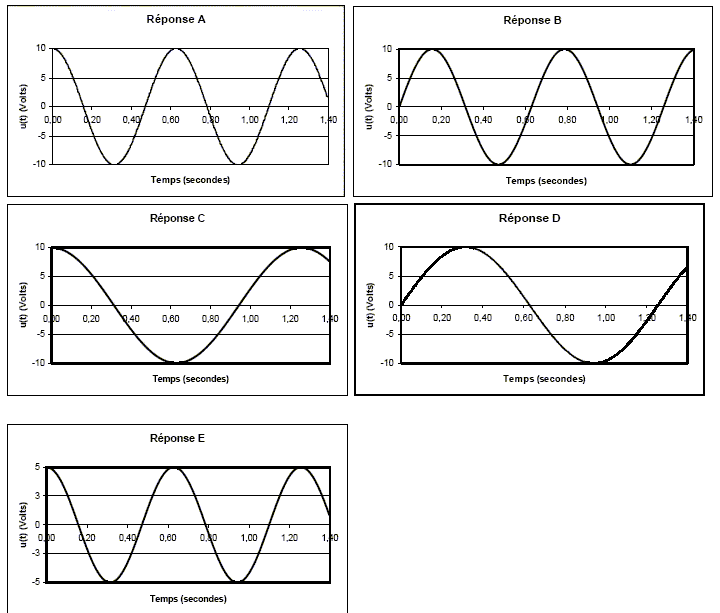
Indiquer l’allure de la tension u(t). La tension à t=0, aux bornes du condensateur est maximale, puis décroît : les courbes B et D sont exclues. période propre du dipole LC : T = 2p(LC)½. T = 2p(10*10-3)½=0,63 s. La courbe C est exclue. La valeur initiale de la tension aux bornes du condensateur est égale à 10 V. La courbe E est exclue. courbe A.
Donner l'amplitude Imax de l'intensité du courant i(t) circulant dans le condensateur et l'inductance. On rappelle que pour t > 0 : i(t) = Imax cos (2pt/T+q) énergie maximale stockée par le condensateur : ½ CE2. énergie maximale stockée par la bobine : ½ LImax2. conservation de l'énergie : CE2 =LImax2 ; Imax = (C/L)½ E = (10-3/10)½ *10 = 0,1 A A. 0,1 A. Vrai. B. 0,5 A. Faux. C. 1A. Faux. D. 5A. Faux. E. 10 A. Faux.
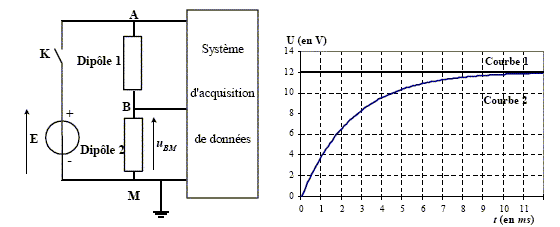
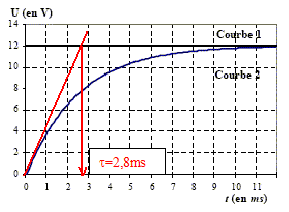
Un système d’acquisition de données mesure les tension uAM (courbe 1) et uBM (courbe 2). A l’instant t = 0, on ferme l’interrupteur K.
Donner l'association de dipoles correspondant à ces courbes : La tension uBM ( courbe 2) est croissante et tend vers une limite égale à E : Le dipole 2 ne peut pas être une bobine inductive, car dans ce cas la tension serait décroissante puis s'annulerait : C. exclu. Le dipole 2 peut être : - Un résistor ( uBM serait l'image de l'intensité au facteur R près ) à condition que le dipole 1 soit une inductance : B. exclu. E. exclu. La constante de temps vaut t = 2,8 10-3 s.
Pour le dipole R L, la constante de temps vaut L/R = 0,3/100= 3 10-3 s. A. vrai. - Un condensateur si le dipole 1 est un résistor. La constante de temps du dipole RC vaut : RC = 104*10-7 = 10-3 s. D. exclu. A. dipole 1 : inductance L = 300 mH dipole 2 : résistance R = 100 W.¶ B. dipole 1 : capacité C = 200 nF dipole 2 : résistance R = 10 kW¶ C. dipole 1 : résistance R = 100 W ¶ dipole 2 : inductance L = 300 mH D. dipole 1 : résistance R = 10 kW¶ dipole 2 : capacité C = 100 nF E. dipole 1 : capacité C = 200 nF dipole 2 : résistance R = 20 kW¶
|
|||
|
|