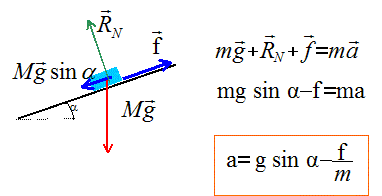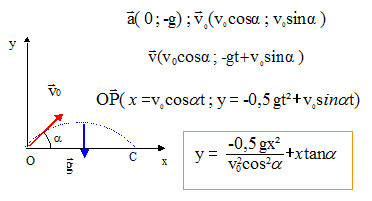concours Fesic plan incliné, pendule, projectile, satellite. 2007

sin 30 = 0,5 ; cos 30 = 0,9 ; tan 30 = 0,6.

A. Pendant le mouvement, le vecteur accélération du solide a une direction parallèle au plan incliné. Vrai.

B. Le vecteur accélération du mobile reste constant pendant toute la durée du déplacement. Vrai.

C. Le travail des forces de frottement pendant le déplacement vaut -0,5 J. Faux.

variation de l'énergie cinétique : 0-½mv² = -0,5 J

Travail moteur du poids en descente sur le parcours d= 1 m : mgd sin a = 1*10*1 *sin 30 = 5 J

Travail résistant des frottements : -fd = -f.

Théorème de l'énergie cinétique : -0,5 = 5 -fd d'où -fd= -5,5 J.

D. La valeur de la force de frottement est f = 5,5 N .Vrai.

-fd = -5,5 ; d = 1 m ; f = 5,5 N

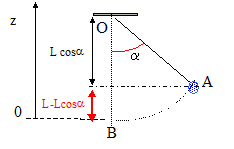
cos 8 = 0,99 ; g = 10 m/s².

A. La période d'un pendule simple est proportionnelle à la racine carrée de sa masse. Faux.

T = 2p [L/g]^½. indépendante de la masse.

B. L'énergie mécanique totale E_m du pendule vaut 1 mJ. Vrai.

Energie mécanique initiale = énergie potentielle de pesanteur = mg L (1-cos a) = 0,01*10*1(1-0,99) = 0,1*0,01 = 10^-3 J = 1 mJ.

C. L'expression de la vitesse maximale est v_max = [2E_m/m]½. Vrai.

Energie mécanique au passage à la position d'équilibre = énergie cinétique = ½mv²_max.

Conservation de l'énergie mécanique : E_m =½mv²_max. ; v²_max. = 2E_m /m.

D. Lorsque l'énergie cinétique du pendule est égale au quart de son énergie mécanique, la vitesse de la masse est égale à la moitié de la vitesse maximale. Vrai.

½mv² = 0,25 E_m =0,125 m v²_max ; v² =0,25   v²_max ; v = 0,5 v_max.

Au jeu de fléchettes, une flèche atteint le centre d'une cible, noté C. Le point C est situé à la même altitude que O, le point de départ de la flèche et à une distance d=100 m du point de départ. L'inclinaison initiale de la flèche par rapport à l'horizontale à la date t=0, initiale, est de 45°. Les frottements sont négligés.

g= 10 m/s² ; cos 45 = sin 45 = 0,7 ; 10^½ = 3,16.

A. La valeur de la vitesse au point C est égale à la valeur de la vitesse initiale. Vrai.

Ecrire le théorème de l'énergie cinétique entre O et C : DEc = ½mv_f²-½mv_i² ;

La flèche n'est soumise qu'à son poids ; les altitudes initiale et finale étant identiques, le poids ne travaille pas. DEc =0

B. Lorsque la flèche atteint son altitude maximale, sa vitesse est égale à la moitié de sa valeur initiale. Faux.

A l'altitude maximale, la composante verticale de la vitesse est nulle ; la vitesse vaut alors v₀ cos a = 0,7 v₀

C. La vitesse initiale de la flèche est 31,6 m/s. Vrai.

abscisse du point C : y_C=0 ; -0,5 g x_C² / ( v₀ cos a)² + x_C sin a / cosa = 0 ;

x_C = v₀² sin ( 2a) / g ; v₀² = gx_C /sin ( 2a) ;

v₀ = [10*100 / sin 90]^½=31,6 m/s.

D. La flèche atteint sa cible au bout de 3,16 s. Faux.

y_C=0 = -½g t² + v₀ sin at ; ½g t = v₀ sin a ; t = v₀ sin a / g = 31,6*0,7/10 = 3,16 *0,7 s.

masse de la terre M= 6,0 10²⁴ kg ; rayon de la terre R= 6,4 10³ km ; G= 6,67 10^-11 S.I

6,67*6 = 40 ; 400 = 7,6²*7.

A. Le vecteur accélération du satellite est centripète. Vrai.

Mouvement circulaire ; altitude constante, donc vitesse de valeur constante

Dans un mouvement circulaire uniforme, l'accélération est centripète est vaut : v²/(R+h).

B. La constante de gravitation G est homogène à des kg^-1 m³ s^-2. Vrai.

F= GMm/(R+h)² : force de gravitation exercée par la terre sur le satellite.

G = F(R+h)² / (Mm) ;

Une force est une masse * une accélération soit une masse * longueur/temps².

Par suite G : kg m s^-2 m² kg^-2 soit : kg^-1 m³ s^-2

C. L'expression de la vitesse du télescope dans le référentiel géocentrique est v = [GM/h]^½. Faux.

v = [GM/(R+h)]^½.

D. Dans le référentiel géocentrique la vitesse du satellite est 7,6 km/s. Vrai.

v = [GM/(R+h)]^½ = [6,67 10^-11*6,0 10²⁴ / ((6,4+0,6 ) 10⁶)]^½ = [6,67 *6,0 10⁷ / 7)]^½

v= [40 10⁷ / 7)]^½= [400 10⁶ / 7)]^½= [7,6² 10⁶ ]^½ = 7,6 10³ m/s.