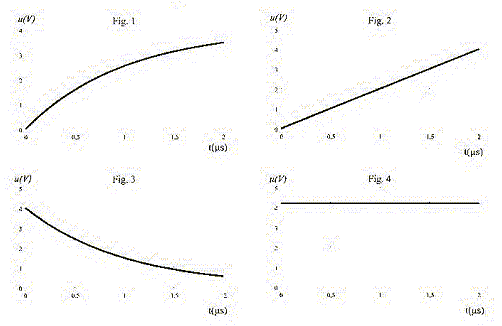Aurélie 17/05/07
 

concours Fesic dipole (LC) ; dipole (RL) ; dipole (RC) . 2007

Google

 

Le circuit ci après est composé d'une source de tension continue E, d'une bobine d'inductance L, d'un condensateur de capacité C, d'un conducteur ohmique R et d'un interrupteur K. Initialement le condensateur et la bobine ne possèdent pas d'énergie.

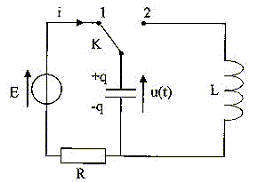
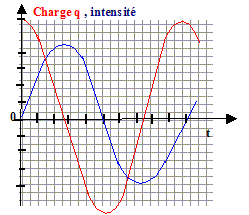
Dans un premier temps, on positionne l'interrupteur K en position 1. Lorsque la tension u(t) atteint la valeur E, on bascule l'interupteur en position 2 ; cet instant est choisit comme origine des temps. Il s'établit alors dans le circuit (L C) un courant sinusoïdal et l'évolution de la charge du condensateur au cours du temps s'écrit :

q(t) = Q cos ( 2pt/T+j). E = 10,0 V ; L= 0,10 H ; C= 0,10 mF.

A. L'intensité i a pour expression i(t) = dq/dt. Faux.

Lors de 1ère décharge du condensateur, q diminue et dq est négatif : i = -dq/dt

Lors de la première charge du condensateur i = dq/dt.

B. A l'instant t= 0+ l'intensité du courant est maximale. Faux.

q(t) = Q cos ( 2pt/T) ; i(t) = Q2p/Tsin( 2pt/T)

C. La période des oscillations est T= 628 ms. Vrai.

T= 2p(LC)½ =2*3,14 (0,1* 10-7)½ =6,28 10-4 s = 628 10-6 s = 628 ms.

D. Dans l'expression q(t) =Q cos ( 2pt/T+j) , j =0 .Vrai.

A t=0, la charge q est positive et maximale : Q = Q cos j d'où cosj = 1 ; j = 0.

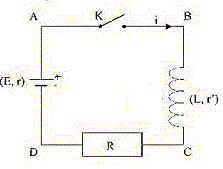
On réalise le circuit suivant comprenant un générateur de tension de f.e.m E et de résistance r, une bobine inductive d'inductance L et de résistance r' et un conducteur ohmique de résistance R. On place un interrupteur K.

A t=0 alors que la bobine n'a pas emmagasiné d'énergie on ferme l'interrupteur K.

E= 9,0 V ; R=87 W ; r= 1,0 W ; r'= 12 W.

A. La constante de temps t du circuit est proportionnelle à L : Vrai.

t = L/(R+r+r') 

B. L'expression de la tension aux bornes de la bobine est uBC= Ldi/dt. Faux.

uBC= Ldi/dt + r' i.

C. A t = 0+ la tension uBC vaut E. Vrai.

Additivité des tensions : uBD = uBC + uCD ;

E-ri = Ldi/dt + r' i + R i ; E= Ldi/dt + (r+r'+R) i

A t=0+ l'intensité est nulle.

D. En régime permanent I= 90 mA. Vrai.

En régime permanent dI/dt = 0 et E = (r+r'+R) I

I= E/(r+r'+R) = 9 / (1+12+87) = 0,09A = 90 mA. 

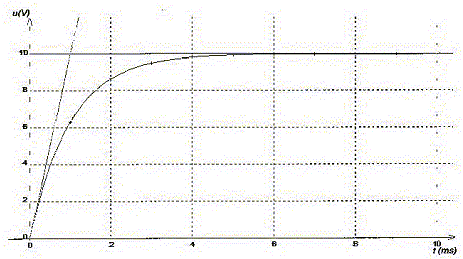
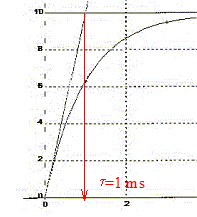
Lors de la charge sous tension constante E d'un condensateur de capacité C à travers un résistor de résistance R ( R= 100 kW), on relève l'évolution de la tension u(t) aux bornes du condensateur. On appelle t la constante de temps du circuit.

A. L'intensité du courant a pour expression i(t) = E/R(1-exp(-t/t)). Faux.

i(t) = E/R exp (-t/t).

B. A l'instant t= 0+ l'intensité vaut 0,10 mA. Vrai.

i(0+) = E/R exp(0) = E/R = 10/105 = 10-4 A = 0,1 mA.

C. La valeur de la capacité du condensateur est 10 mF. Faux.

RC= 10-3 ; C= 10-3/R = 10-3/105 = 0,01F = 10 mF

D. C étannt la capacité du condensateur, le générateur doit fournir l'énergie W= 50C pour que le condensateur soit chargé. Faux.

énergie élémentaire fournie par le générateur pendant la durée dt : dW =E idt avec i = dq/dt ; dW = E dq

W= EQ avec Q= C E ; W= CE2 = 100 C. E= 10 V, tension aux bornes du condensateur chargé ( lecture graphe).

Un condensateur de capacité C, initialement déchargé, est chargé grâce à un générateur idéal de courant d'intensité constante I=0,2 A.

Une acquisition informatique a permis de tracer l'évolution temporelle de la tension u aux bornes du condensateur lors de la charge. Hélas ce document s'est mélangé à trois autres.

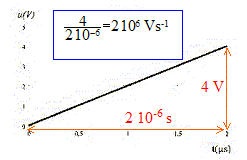
A. La figure 1 constitue le document cherché. Faux.

Q= It ; Q= Cu avec u tension aux bornes du condensateur

It = Cu soit u = I/C t ; droite de coefficient directeur I/C ( figure 2)

B. La capacité du condensateur est C= 0,10 mF. Vrai.

I/C=2 106 ; C= I/2 106 = 0,2/2 106 = 10-7 F = 0,1 mF

On arrête la charge du condensateur à la dat t1 lorsque celui-ci porte la charge 0,20 m C.

C. La tension aux bornes du condensateur vaut 2,0 V. Vrai.

Q=C U ; U= Q/C = 2 10-7 / 10-7 = 2,0 V.

D. L'énergie emmagasinnée à la date t1 est alors 4,0 107 J. Faux.

½ Q2/C =(2 10-7)2/ 10-7 = 4 10-7 J

  
 

retour -menu