|
|
|||||||||
|
|||||||||
|
A- L'unité eV est homogène à C V. Vrai. Une énergie peut s'exprimer en eV. énergie (J) = tension (V) * intensité (A) * temps (s) =tension (V) *quantité d'électricité (C) B- L'unité mol est homogène à kg . Faux. quantité de matière (mol) = masse (g) / masse molaire (g/mol) C- Une énergie s'exprime en kg m2 s-2. Vrai. énergie, travail d'une force (J) = force (N) * longueur (m) or force (N) = masse (kg) * accélération (m s-2) D- Un défaut de masse s'exprime en mol. Faux. en kg ou en u. E- Une TEP tonne équivalent pétrole est une unité d'énergie . Vrai. Masse d'un combustible produisant autant d'énergie qu'une tonne de pétrole. Vrai du point de vue industriel et économique.
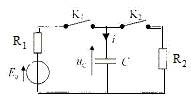
De t=0 à T K1 est fermé
et K2 est ouvert. T est suffisamment
long pour charger complètement le
condensateur. A- L'intensité initiale du courant est nulle. Faux. additivité des tensions à la date t=0 : E0 = R1 i(0) + uC (0) ; or uC(0) = 0 d'où i(0) = E0/R1. B- La tension finale aux bornes du condensateur est nulle. Faux. La tension finale aux bornes du condensateur vaut E0. A partir de t=T, K1 est ouvert et K2 est fermé. C- L'intensité initiale lors de la décharge est nulle. Faux. Le courant change de sens. additivité des tensions à la date t=T+ : 0= R2i(T+) + uC (T+) ; or uC(T+) = E0 d'où i(T+) = -E0/R2. D- La tension uC à la date t =T+ vaut -E0. Faux. Continuité de la tension aux bornes du condensateur uC(T+) =uC(T-) = E0 E- La constante de temps du circuit entre [0 ; T) est la même qu'à t >T . Faux. t1 = R1C et t2 = R2C avec R1différent de R2.
A- Lénergie accumulée dans le condensateur à t=T vaut 8 10-5 J. Vrai. Le condensateur est chargé ; la tension à ses bornes vaut E0=4 V. ½CE02 = 0,5*10-5*16 = 8 10-5 J B- L'énergie dissipée par effet joule de t=0 à T à travers R1 vaut 8 10-5 J. Vrai. Energie dissipée par effet Joule dans R1 pendant la durée dt : dW =R1i2dt avec i = E0/R1 exp(-t/t) ; t = R1C = 10-4 s ; T= 10t. dW= R1(E0/R1)2exp(-2t/t)dt intégrer entre 0 et 10t : E02/R1 (-½ t )[exp(-2t/t)]010t =E02/R1 (½ t ) = 16/10 * 5 10-5 = 8 10-5 J C-L'énergie fournie par le générateur de t=0 à t=T vaut 8 10-5 J. Faux. L'énergie fournie par le générateur est égale à la somme de l'énergie stockée par le condensateur et de l'énergie dissipée par effet joule. soit 16 10-5 J. A partir de t=T, K1 est ouvert et K2 est fermé. D- L'énergie accumulée par le condensateur à t=T vaut 16 10-5 J. Faux. 8 10-5 J E- L'énergie dissipée par effet joule à travers R2 vaut 16 10-5 J. Faux. Elle est égale à l'énergie stockée initialement par le condensateur soit 8 10-5 J.
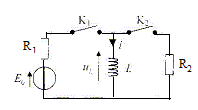
A- L'intensité initiale est nulle. Vrai. La bobine s'oppose à l'établissement du courant à la fermeture de K1. B- La tenion finale aux bornes de la bobine est nulle. Vrai. uL= Ldi/dt ; uL(T) = L[di/dt ]T ; en régime permanent [di/dt ]T =0. A partir de t=T, K1 est ouvert et K2 est fermé. C- L'intensité à la date t = T+est nulle. Faux. A t =T+ , I(T)=I(T+)= E0/R1. Continuité de l'intensité. D- La tension aux bornes de la bobine est nulle à la date t=T+. Faux. Discontinuité de la tension aux bornes de la bobine : uL(T+) + R2I(T+) = 0 ; uL(T+) =- R2I(T+) = - R2E0/R1. E-La constante de temps du circuit entre [0 ; T) est la même qu'à t >T . Faux. t1 = L/R1 et t2 = L/R2 avec R1différent de R2.
Le régime permanent est établi et I = E0/R1 = 4/10 = 0,4 A ½LI2 = 0,5*0,01*0,42 = 8 10-4 J B- L'énergie dissipée dans R1 de t=0 à T vaut 8 10-4 J. Faux. Energie dissipée par effet Joule dans R1 pendant la durée dt : dW =R1i2dt avec i = E0/R1(1- exp(-t/t)) ; t = L/R1 = 10-3 s ; T= 10t. dW= R1(E0/R1)2(1- exp(-t/t))2dt = R1(E0/R1)2[dt + exp(-2t/t)dt -2exp(-t/t)dt] intégrer entre 0 et 10t : E02/R1 [t + (-½ t ) exp(-2t/t)+ 2t exp(-t/t)]010t =E02/R1 [10 t+½ t -2 t]010 t. E02/R1 (8,5 t ) = 16/10 * 8,5 10-3 = 136 10-4 J. C- L'énergie fournie par le générateur de t=0 à T vaut 16 10-4 J. Faux. Energie fournie par le générateur pendant la durée dt : dW =E0idt avec i = E0/R1(1- exp(-t/t)) dW = E02/R1(1- exp(-t/t))dt intégrer entre 0 et 10t : E02/R1 [t +t exp(-t/t)]010 t = E02/R1 (10 t-t ) = E02/R1 (9t )= 16/10*9 10-3 = 144 10-4 J. A partir de t=T, K1 est ouvert et K2 est fermé. D-L'énergie accumulée par la bobine à t = T+ est 2 10-4 J. Faux. L'énergie stockée à la date t=T est identique à l'énergie stockée à la date t=T+. E-L'énergie dissipée par effet joule à travers R2 vaut 2 10-4 J. Faux. Elle est égale à l'énergie stockée à t=T+ par la bobine soit 8 10-4 J.
|
|||||||||
|
|
|||||||||
|
|