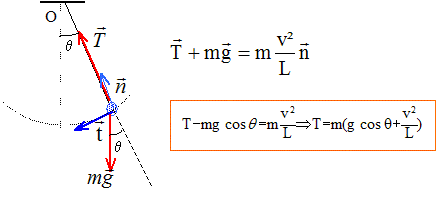concours Esiee th de l'énergie cinétique ; lois de Newton; travail d'une force; oscillateurs mécaniques 2007

Aurélie 11/05/07

Les vecteurs sont écrits en gras et en bleu.

Une masse m, considérée ponctuelle, est lancée de A avec une vitesse initiale v₀i. Elle parcourt d'abord la portion horizontale AB=d puis s'engage sur un plan incliné d'un angle a par rapport à l'horizontale. En outre m subit dès le départ et sur tout son trajet, un force de frottement de type -F u où F est une constante et u un vecteur unitaire colinéaire au vecteur vitesse. On note g l'accélération de la pesanteur.

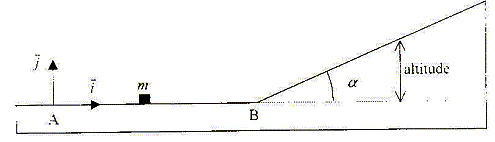
v₀ = 4 m/s ; m = 100 g ; d= 7 m ; F=0,05 N; g = 10 m/s² ; sin a =0,1.

A- m arrive en B avec une vitesse de 3 m/s. Vrai.

Th. de l'énergie cinétique entre A et B .

m est soumise à son poids, à l'action du support et à la force de frottement : le poids et l'action du plan, perpendiculaires à la vitesse ne travaillent pas.

Travail résistant des frottements W = -F AB = -F d = -0,05*7 = -0,35 J.

DEc = ½mv_B² - ½mv₀² = -0,35 ; v_B² = v₀² - 2*0,35 / m ; v_B² =16-0,7/0,1 = 9 ; v_B= 3 m/s.

B- m parcourt AB en 1,75 s. Faux.

Ecrire la seconde loi de Newton selon i : -F = m a ; a = -F/m = -0,05/0,1 = -0,5 m/s².

vitesse v(t) = at + v₀ ; v(t) =-0,5 t + 4 ; t_B =( 4-v_B) / 0,5 ; t_B = 2 s.

C- m atteint l'altitude maximale 8 s après son lancement. Faux.

Sur le plan incliné, m est soumise à son poids, à l'action du plan perpendiculaire au plan et au frottements.

Ecrire la seconde loi de Newton selon un axe parallèle au plan dirigé vers le haut du plan :

-mg sin a - F = ma ; a = -( g sin a + F/m) = -(10*0,1+0,05/0,1) ; a = - 1,5 m/s².

vitesse v(t) = at+v_B ; v(t) = -1,5 t +3

A l'altitude maximum il y a arrêt ( vitesse nulle) d'où t_arrêt = 2 s.

Durée totale du parcourt : 4 s.

D- m atteint l'altitude maximale de 30 cm. Vrai.

( origines : le passage en B) : distance parcourue sur le plan z(t) = ½at² + v_Bt ;

z = 0,5(-1,5) 2²+3*2 = 3 m.

altitude atteinte = distance parcourue * sin a = 3*0,1 = 0,3 m = 30 cm.

E- 4 s après son lancement, la vitesse de m est 2m/s. Faux.

La durée totale du parcours avant arrêt est de 4 s.

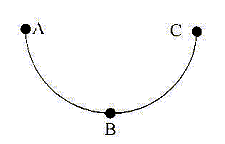
Un coureur parcourt une pisete circulaire ( ABCDA) Il part de A sans vitesse initiale et percourt le premier quart de la piste avec une vitesse dont la norme augmente proportionnellement au temps soit v = g₁t. Il parcourt le reste avec un mouvement circulaire uniforme, c'est à dire à la vitesse atteinte en B. Le rayon du cercle est R= 300/p mètre et g₁= 1/ 3 m /s².

A- Le coureur effectue le premier quart de tour en 30 s. Vrai.

v = g₁t ; x= ½ g₁t² ; t = [2x/g₁]^½ avec x = ½pR = 150 m.

t = [300*3]^½ = 30 s.

B- Sa vitesse en B vaut 10 m/s. Vrai.

v_B= g₁t = 30/3 = 10 s.

C- Le coureur effectue les trois derniers quarts de tour en 45 s. Vrai.

distance : 1,5 pR = 450 m ; vitesse : 10 m/s

durée du mouvement uniforme : 450 / 10 = 45 s.

D- La vitesse angulaire du coureur pendant les trois derniers quarts de tour est w= 6 rad/s. Faux.

w = v/R = 10 p/300 = p/30 rad/s.

E- L'accélération du coureur en D vaut p/3 m/s². Vrai.

L'accélération centripète vaut : v²/R = 100 *p/300 = p /3 m/s².

Un anneau de masse m glisse sans frottement sur un arc métallique ABC en forme de demi-cercle de rayon R= 10/p mètre. Outre le poids P et la réaction de l'arc sur l'anneau, deux forces F et F' d'intensité constantes de 100 N et 157 N respectivement agissent sur l'anneau.

F reste tangente au cercle et dans le sens opposé au mouvement. F' agit selon la direction horizontale et de la gauche vers la droite.

On note W_XY(f) le travail d'une force f) sur le chemin menant de X à Y. On prend p = 3,14.

A- W_AB(F) = -500 J. Vrai.

Puissance de F à la date t : P = F. v = -Fv ( vecteurs colinéaires de sens contraire)

travail élémentaire sur le parcours noté ds = v dt : dW= -F v dt = -F ds

Travail sur le parcours AB de longueur ½pR = 5 m : W_AB(F) = -½pR F =-5*100 = -500 J.

B- W_AB(F) = W_BC(F). Vrai.

F et v vecteurs colinéaires de sens contraire ; F garde la même valeur ; le parcours a la même longueur.

C- W_AB(F') = 500 J. Vrai.

Le travail d'une force constante ne dépend que des positions initiale et finale.( on choisit le parcours AO B avec O centre du cercle )

W_AB(F') = W_AO(F') + W_OB(F') = AO * F' + 0 ( F' perpendiculaire à OB)

W_AB(F') = R F' = 10/p*157 =1570/3,14 = 500 J.

D- W_AB(F') = W_BC(F'). Vrai.

W_BC(F') = W_BO(F') + W_OC(F') = 0+OC * F'= R F'.

E- W_AB(P) = W_BC(P). Faux.

Le travail d'une force constante ne dépend que des positions initiale et finale.( on choisit les parcours AO B et BO C avec O centre du cercle )

Travail moteur du poids en descente de O vers B ; travail résistant du poids en montée de B vers O.

Une masse m est attachée à l'extrémité d'un ressort sans masse de constante de raideur k et de longueur à vide L₀. L'autre extrémité est fixée en O à un support immobile. On néglige tout frottement. On note x=OM la position de m sur l'axe Ox orienté vers le bas. On note g l'accélération de la pesanteur supposée constante.

En O l'énergie potentielle de pesanteur est prise égale à 0.

A- La position d'équilibre de m correspond au minimum d'énergie potentielle élastique. Faux.

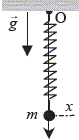
La position d'équilibre correspond à un minimum de l'énergie potentielle totale ( énergie potentielle élastique et énergie potentielle de pesanteur)

Energie potentielle de pesanteur : -mgx ( origine en O)

Energie potentielle élastique : : ½k(x-L₀)².

Energie potentielle totale : E_p= ½k(x-L₀)²-mgx.

B- A la position d'équilibre de m, la somme des énergies potentielles est nulle. Faux.

La position d'équilibre correspond à un minimum de l'énergie potentielle totale.

dEp/dx= 0 donne k(x_mini-L₀)-mg soit x_mini = mg/k + L₀.

E_{p mini} = ½k(x_mini-L₀)²-mgx_mini = (mg)²/ (2k) -(mg)²/ k -mgL₀ =-(mg)²/ (2k) -mgL₀ = -mg(mg/(2k)+L₀).

C- La position d'équilibre de m correspond à x_E= L₀+mg/k. Vrai.

A la position d'équilibre le poids de m compense la tension du ressort.

mg = k(x_E-L₀) ; x_E =mg/k + L₀

La longueur du ressort est L= L₀+mg/k.

On lache m de A, x_A > x_E, sans vitesse initiale, m oscille alors en restant sur l'axe Ox entre les positions A et B.

D- L'énergie cinétique de m est maximale lorsque l'énergie potentielle élastique est nulle. Faux.

L'énergie mécanique se conserve ; l'énergie mécanique est la somme de l'énergie cinétique et de toutes les énergies potentielles.

L'énergie cinétique est maximale lorsque l'énergie potentielle totale est minimale, c'est à dire à la position d'équilibre.

Mais à la position d'équilibre l'énergie potentielle élastique vaut : ½k(x_éq-L₀)².

½k(mg/k + L₀-L₀)² = (mg)²/ (2k)

E- Quand la masse m passe à la position d'équilibre, la vitesse est maximale. Vrai.

A la position d'équilibre l'énergie potentielle totale étant minimale, l'énergie cinétique est maximale : en conséquence la vitesse est maximale.

Un pendule simple est constitué d'une masse m attachée à un fil inextensible, sans masse et de longueur L. Lâchée de A sans vitesse initiale, m oscille alors dans un plan vertical entre les positions extrèmes A et B quand on néglige tout frottement.

On se place dans le cas des petites oscillations. ( q reste faible et on confond sin q avec q en radian )

A- La période du mouvement dépend de m. Faux.

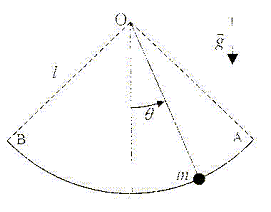
T = 2p [L/g]^½.

B- La période du mouvement est proportionnelle à L. Faux.

C- La vitesse maximale atteinte est indépendante de m. Vrai.

th de l'énergie cinétique entre A et M : DEc=½mv² - 0

La tension du fil perpendiculaire à la vitesse ne travaille pas.

travail du poids ( de A vers M) ; origine des altitudes : la position d'équilibre)

W = mgL(cosq- cos q_A).

½mv² = mgL(cosq- cos q_A) ; v² =2gL(cosq- cos q_A)

D- La tension du fil est de norme constante au cours du mouvement. Faux.

E- La fréquence du mouvement est indépendante de m.Vrai.

La fréquence est l'inverse de la période ; la période est indépendante de m.

retour -menu