Aurélie 10/05/07
 

concours EPF ondes ; radioactivité : datation au carbone 14. 2006

Google

Ondes : 

Répondre par vrai ou par faux en justifiant brièvement :

- La longueur d'onde est la distance parcourue par l'onde en 1 s. Faux.

" distance parcourue par l'onde durant une période ".

- La vitesse de propagation d'une onde ne dépend pas du type d'onde ni du milieu de propagation. Faux.

Dans un milieu dispersif la vitesse dépend de la fréquence de l'onde.

- La vitesse de propagation d'une onde électromagnétique est d'autant plus grande que le milieu est peu dense. vrai.

v = c/n ; quand n tend vers 1, alors v tend vers c.

- La vitesse d'une onde sonore est la même dans l'air que dans le vide. Faux.

L'onde sonore ne se propage pas dans le vide.

Archéologie, datation au carbone 14.

Les deux isotopes du carbone 126C et 146C existent dans la nature. Le "carbone 14", radioactif b-, est formé continuellement dans la haute atmosphère et on suppose que la proportion de cet isotope est restée constante au cours des derniers millénaires.

  1. Ecrire l'équation de désintégration du carbone 14.
  2. Le temps de demi-vie du carbone 14 est 5570 ans. Définir le temps de demi-vie.
  3. On appelle N0 le nombre de noyaux radioactifs d'un échantillon à un instant pris comme origine des dates.
    - Exprimer, en fonction de N0, le nombre de noyaux N de carbone 14 restant aux instants de dates t1/2, 2t1/2, 3t1/2, 4t1/2 et 5t1/2.
    - Tracer l’allure de la courbe représentant le nombre N de noyaux radioactifs en fonction du temps après avoir placé les points définis.
  4. Tant que la matière est vivante, les échanges de l’organisme animal ou végétal impliquant le dioxyde de carbone atmosphérique font que le rapport N( 146C) / N( 126C) reste constant. A la mort de l’être vivant, la fin de ces échanges entraîne une décroissance de ce rapport.
    - Ecrire la loi de décroissance du nombre de noyaux radioactifs en fonction du temps. Expliciter tous les termes employés.
    - Démontrer la relation entre le temps de demi-vie t1/2 et la constante radioactive l.
    - Des ossements appartenant à deux hommes, nommés A et B, ont été retrouvés sur un site archéologique. Les fractures observées sur les ossements de A permettent de supposer que B est l’assasin de A. L’analyse des ossements donne les résultats suivants :
    Nature des échantillons
    N/N0
    échantillons prélevés sur les ossements de A
    1,34 10-2
    échantillons prélevés sur les ossements de B
    1,87 10-2
    B peut-il être l’assassin de A ? (Calculer l’age des ossements de A et de B).

équation de désintégration du carbone 14.

146C = 147N + 0-1e

conservation du nombre de nucléons : 14= 14 +0

conservation de la charge : 6 = 7-1

temps de demi vie ou période :

durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.
t½
2t½
3t½
4t½
5t½
0,5N0
0,25N0
0,125N0
0,0625N0
0,0312N0

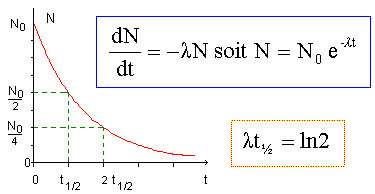
Loi de décroissance du nombre de noyaux radioactifs en fonction du temps.

N(t) = N0 exp(-lt)

N(t) : nobre de noyaux présents à la date t ; N0 : nombre de noyaux présents à la date origine t0.

l: constante radioactive, inverse d'un temps ; t: temps ( en seconde)

Relation entre le temps de demi-vie t1/2 et la constante radioactive l :

à t½, N(t) = 0,5 N0 soit : 0,5 N0 = N0 exp(-lt½)

0,5 = exp(-lt½) ; ln(0,5 ) = -lt½ ; ln 2 = lt½

Age des ossements de A et de B :

l = ln2 / t½ = 0,693 / 5570 = 1,244 10-4 an-1

A : 0,0164 = exp(-lt) ; ln (0,0164) = -4,11 = -lt

t = 4,11 / l = 4,11 / 1,244 10-4 = 33 038 ans.

B : 0,0187 = exp(-lt) ; ln (0,0187) = -3,979 = -lt

t = 3,979 / l =3,979 / 1,244 10-4 = 31 987 ans.

1000 ans d'écart, la réponse est "non "dans la mesure ou cette méthode de datation est très précise.

 
 

retour -menu