Aurélie 21/05/07
 

Diplome d'accès aux études universitaires B radioactivité: plutonium 238, projectile 2005

Google

 

Exercice 2 (7 points)

Données :

extrait de la classification

90Th, 91Pa, 92U, 93Np, 94Pu ;

masse molaire atomique du plutonium M = 238 g.mol-1 ;

constante d'Avogadro NA = 6,02 1023 mol-1 .

Un stimulateur cardiaque contient une masse m = 150 mg de l'isotope 238 de plutonium émetteur a de demi-vie t½, avec t½ = 87,8 ans. La source de plutonium, très petite, est hermétiquement scellée dans un récipient. A partir de l'énergie libérée par chaque désintégration, le stimulateur produit une puissance électrique.

  1. Écrire, en précisant les lois de conservation utilisées, la réaction de désintégration du plutonium 238. Quels sont les rayonnements émis lors de la désintégration ?
  2. Calculer le nombre de noyaux N0 initialement présents dans le stimulateur. En déduire l'activité initiale A0 du stimulateur cardiaque.
  3. Donner la loi de décroissance de l'activité en fonction du temps. Donner l'allure de la courbe pour une durée t allant de 0 à 100 ans.
  4. On considère que le stimulateur fonctionne de façon satisfaisante jusqu'à une diminution de 30 % de son activité. Quelle est, dans ces conditions, sa durée de vie ? Calculer alors le nombre de noyaux N de plutonium restant.
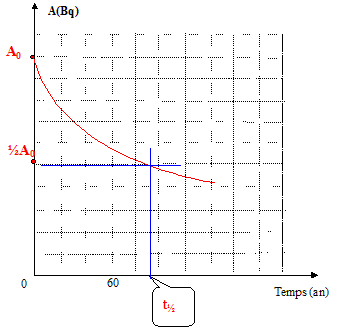
Réaction de désintégration du plutonium 238 :

Une particule a, ou noyau d'hélium 42He est émise.

23894Pu ---> 42He +AZX*.

Conservation de la charge : 94=2+Z d'où Z = 92 ( élément uranium)

Conservation du nombre de nucléons : 238=4+A d'où A = 234.

Le noyau fils peut être dans un état excité et émettre un photon g lors du retour à l'état fondamental.

23492U*---> 23492U +00g

Nombre de noyaux N0 initialement présents dans le stimulateur :

quantité de matière (mol) = masse (g) / masse molaire (g/mol) : n= 0,15/238 = 6,30 10-4 mol

N0 = n NA = 6,30 10-4 *6,02 1023 = 3,79 1020 noyaux.

Activité initiale A0 du stimulateur cardiaque :

La constante radioactive l vaut l = ln2/t½ avec t½ = 87,8*365*24*3600 =2,77 109 s.

l = ln2 / 2,77 109 = 2,50 10-10 s-1.

A0 =lN0 = 2,50 10-10 *3,79 1020 = 9,49 1010 Bq.

Loi de décroissance de l'activité en fonction du temps :

A(t) = A0 exp(-lt)

Allure de la courbe pour une durée t allant de 0 à 100 ans :

On considère que le stimulateur fonctionne de façon satisfaisante jusqu'à une diminution de 30 % de son activité.

Sa durée de vie : A= 0,7 A0 ;

0,7 A0; = A0 exp(-lt) ; ln 0,7 =- lt ;

t= ln 0,7 /(- l) = ln 0,7 /(-2,50 10-10)

t= 1,43 109 s = 45,3 ans.

Nombre de noyaux N de plutonium restant :

A= 0,7 A0 = l N ; N = 0,7 A0 / l ;

N= 0,7*9,49 1010 / 2,50 10-10

N= 2,66 1020 noyaux.

Exercice 3 (6 points)

Valeur du champ de pesanteur : g = 9,8 m.s-2.

Un joueur de pétanque lance une boule de masse m d'un point B situé à une hauteur OB = hB = 1,5 m au-dessus du sol.

Le vecteur vitesse initiale vB de la boule fait un angle a = 60° avec l'horizontale.

La boule atteint le sol à une distance d = 7,2 m de la verticale du point B.

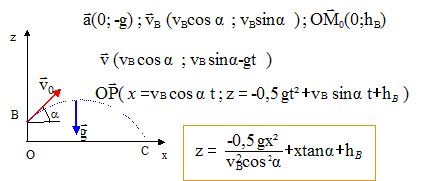
  1. Trouver l'équation de la trajectoire du centre d'inertie G de la boule dans le repère (0; i, j, k ).
  2. Calculer la valeur de la vitesse initiale.

Le mouvement s'effectue dans le plan contenant l'accélération et le vecteur vitesse initiale ; donc y=0.

z= -0,5*9,8 x2 /(vB2 cos260) + x tan 60 + 1,5

z = -19,6 x2 /vB2+1,73 x +1,5.

Valeur de la vitesse initiale :

 Au point C: y=0 et x = 7,2 m.

0 = -19,6*7,22/vB2 +7,2*1,73+1,5

-1016 /vB2 +13,96 = 0 ;

vB2 = 1016/13,96 =72,78 ; vB= 8,5 m/s.

 

retour -menu