Aurélie 29/05/07
 

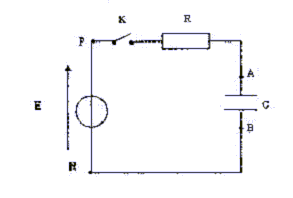
concours ergothérapie dipole RC, charge d'un condensateur. Créteil 2007

6 points ; durée : 20 min.

Google

 

On considère le circuit suivant comprenant, montés en série : un générateur de tension continue de fem E= 10 V et de résistance interne nulle, une résistance R= 1,0 kW, un condensateur de capacité C et un interrupteur K.

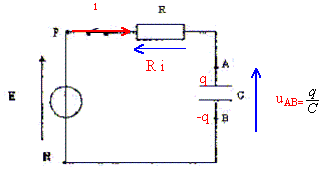
Etablir avec rigueur l'équation différentielle liant la tension uAB(t) aux bornes du condensateur et sa dérivée par rapport au temps duAB/dt en fonction de R, C et E.

Vérifier que l'expression uAB (t) = E(1-exp(-t / (RC))) est bien solution de l'équation différentielle.

Le condensateur possède une tension uAB= 6,3 V au bout de 0,10 ms. En déduire, en justifiant la valeur de la capacité C ( en nF).

Quelle est la valeur de la tension uAB(t) à t= 1 ms ? Justifier. En déduire l'expression littérale de l'énergie emmagasinée dans le condensateur puis sa valeur numérique en mJ.

En utilisant la solution de l'équation différentielle exprimer CduAB/dt et en déduire la valeur de l'intensité du courant quand t devient très grand.

 

Equation différentielle liant la tension uAB(t) aux bornes du condensateur :

additivité des tensions : E = Ri + uAB(t)

Or i = dq/dt et q= cuAB(t) d'où i = CduAB(t)/dt.

E= RCduAB(t)/dt + uAB(t). (1)

Vérifions que l'expression uAB (t) = E(1-exp(-t / (RC))) est bien solution de l'équation différentielle.

duAB(t)/dt = E/(RC) exp(-t/(RC))

Repport dans (1) : E= E exp(-t/(RC)) + E(1-exp(-t / (RC)))

Cette égalité est vérifiée quelque soit t : la fonction uAB (t) = E(1-exp(-t / (RC))) est solution de l'équation différentielle.

Valeur de la capacité C ( en nF) :

Le condensateur possède une tension uAB= 6,3 V au bout de 0,10 ms.

Au bout d'une durée égale à la constante de temps t =RC, la tension aux bornes du condensateur est égale à 63 % de sa valeur finale ( 10 V dans ce cas).

Donc t = 0,1 ms = 10-4 s.

C= t /R avec R= 103 W.

C= 10-4 / 103 = 10-7 F = 100 10-9 F ; C= 100 nF.

Valeur de la tension uAB(t) à t= 1 ms :

t/ t = 10-3/10-4 = 10 ; exp(-10) = 4,5 10-5 ; 1-4,5 10-5 = 0,99995 ; uAB(1ms) = 9,9995 V

uAB(1ms) =E = 10 V.

Energie emmagasinée dans le condensateur :

½CE2 = 0,5*10-7*100 = 5 10-6 J = 5 mJ.

Expression CduAB/dt et valeur de l'intensité du courant quand t devient très grand :

duAB(t)/dt = E/(RC) exp(-t/(RC))

i = dq/dt = CduAB(t)/dt = E/R exp(-t/(RC)).

Valeur de l'intensité du courant quand t devient très grand :

exp(-t/t) tend vers zéro quand t devient très grand : l'intensité tend donc vers zéro.

 

retour -menu