Concours Kiné : de l'inclinaison pour un ressort 2007 ( Ceerrf)

Aurélie 03/04/07

Question 3 : 14 pts/40 sans calculatrice

Soit un ressort à spires non jointives, de raideur k et de longueur au repos L0, dont les extrémités sont reliées à un point fixe O s'un plan incliné et à un point M de masse m. Le plan incliné fait un angle a par rapport à l'horizontale. On pose x = abscisse de M ; il n'y a pas de frottement de glissement sur le plan.

Sans justification écrire l'équation différentielle pour le mouvement d'un oscillateur élastique horizontal, libre, non amorti, en fonction de m, k et x.
La masse m est en équilibre :
- Indiquer les forces qui agissent sur M. Faire un schéma.
- Donner l'expression de ces forces dans le repère (O, x, y).
- Déterminer l'expression de l'abscisse x_eq du point M.
A partir de la position d'équilibre, le ressort est étiré de D>0 et relâché sans vitesse initiale.
- Etablir l'équation différentielle du mouvement de M en fonction de x, k, m et x_eq.
- Pour retrouver l'équation différentielle type de la question 1, on change de repère par une translation judicieuse et on note X l'abscisse de M dans ce nouveau repère. Ecrire la relation entre X et x.
- En déduire l'équation différentielle du mouvement de M en fonction de X, k et m.
- Déterminer X(t) en fonction de D, k et m. On choisira pour cela la solution habituelle ( fonction cosinus) en fonction de la période propre T₀ de l'oscillateur.
- En déduire x(t) en fonction de D, k, m, g, L₀ et a.
Sous la forme d'un tableau, donner les expressions ou valeurs de v(t) aux dates 0,25 T₀ , ½T₀, 0,75 T₀ et T₀.

Equation différentielle pour le mouvement d'un oscillateur élastique horizontal, libre, non amorti, en fonction de m, k et x.

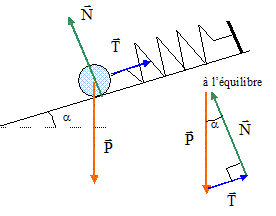
x"+k/mx=0 (1)

La masse m est en équilibre sous l'action du poids ( valeur mg) de la tension du ressort et de l'action du plan.

Expression de ces forces dans le repère (O, x, y):

poids ( mgsina ; - mg cosa) ; action du plan ( 0 ; N= mg cosa ) ; tension ( -k(x-L₀) ; 0)

Expression de l'abscisse x_eq du point M :

à l'équilibre sin a = T/P = k(x_éq-L₀)/mg ; x_éq = L₀+mgsina / k.

A partir de la position d'équilibre, le ressort est étiré de D>0 et relâché sans vitesse initiale.
Equation différentielle du mouvement de M en fonction de x, k, m et x_eq :

Ecrire la seconde loi de Newton sur l'axe des abscisses : mgsina -k(x-L₀) = mx".

mgsina -k(x-x_éq+x_éq-L₀) = mx".

mgsina -k(x-x_éq)-k(x_éq-L₀) = mx". Or mgsina =k(x_éq-L₀)

d'où mx"+k(x_éq-L₀) =0 ; x"+k/ m (x-x_éq) =0.

Pour retrouver l'équation différentielle type de la question 1, on change de repère par une translation judicieuse et on note X l'abscisse de M dans ce nouveau repère. L'origine du nouveau repère est la position d'équilibre. La relation entre X et x est X= x-x_éq.
Equation différentielle du mouvement de M en fonction de X, k et m :

remarque X"=x" ; X" + k/mX=0.

solution de cette équation : X(t) = D cos ( 2pt/T₀).

x(t) = X(t) + x_éq = D cos ( 2pt/T₀) + L₀+mgsina / k.

Expressions ou valeurs de v(t) aux dates 0,25 T₀ , ½T₀, 0,75 T₀ et T₀.

v(t) = dX/dt = -D2p/T₀ sin ( 2pt/T₀).

dates 0,25 T₀ ½T₀ 0,75 T₀ T₀

v(t) -D2p/T₀ 0 D2p/T₀ 0

retour -menu