Concours Kiné : distance focale d'une lentille 2007 ( Ceerrf)

Aurélie 03/04/07

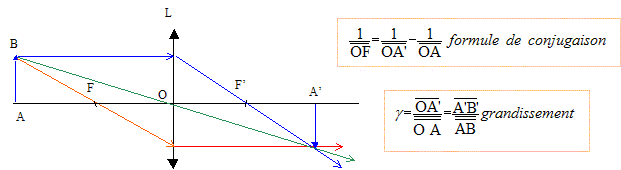
Question 1 : 14 pts/40 sans calculatrice

Les distances algébriques sont écrites en gras et en bleu.

I. On considère une lentille mince convergente (L) qui donne d'un objet AB = 2 cm situé à sa gauche, une image notée A'B', située à la distance AA'= 40,0 cm de l'objet. Dans ces conditions l'image est telle que A'B' = 2 cm.

L'image est elle droite ou renversée ?
Etablir rigoureusement la relation entre la distance D=AA' et la distance focale notée f' de la lentille.
Calculer cette distance focale. Donner l'expression de la vergence C de la lentille.

II. On souhaite obtenir une lentille équivalente à L en accolant deux lentilles minces identique L' de vergence C'.

Etablir avec rigueur l'expression de la vergence C_ass de la lentille unique équivalente à l'association des deux lentilles minces accolées, de vergence respectives C₁ et C₂.
Une lentille L' seule donne d'un objet AB situé 30 cm à sa gauche, une image A'B' située à 90 cm de A à droite de l'objet. Vérifier par le calcul que la distance focale image de cette lentille coincide avec le résultat du 1.

III. La lentille L est utilisée seule. On place l'objet ( le même qu'en I.) 5 cm à sa gauche.

Construire l'image A₁B₁ de AB au travers de L.
Déterminer en justifiant les caractéristique de l'image.
Retrouver ces caractéristiques par le calcul.
L'objet AB est en réalité une pièce de monaie. Déterminer le diamètre de cette pièce ( en mm ) sachant que l'image que donne la lentille de cette pièce a une surface de 12 cm².
On souhaite prolonger la vision de A₁B₁ sans fatigue pour l'oeil. Où doit se trouver A₁B₁ ? Même question pour AB ? ( Justifier à l'aide d'une construction).
- De quelle distance et dans quel sens faut-il déplacer la lentille ?

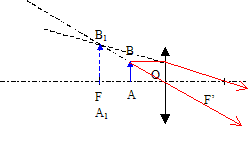
L'image est réelle, renversée.

Relation entre la distance D=AA' et la distance focale notée f' de la lentille :

D= AO+ OA' ; g =-1 = OA' / OA ; OA = -OA' ; AO =OA'

D= OA' +OA' ; OA' = ½ D. OA = - ½ D.

1/OF' = 2/D + 2/D = 4 /D ; OF' =D/4= 10 cm = 0,10 m.

La vergence vaut C=1/f' = 1/0,1 = 10 d.

Expression de la vergence C_ass de la lentille unique équivalente à l'association des deux lentilles minces accolées, de vergence respectives C₁ et C₂.

La première lentille L₁ donne d'un objet réel AB une image A₁B₁ telle que : C₁ = 1/OA₁-1/OA.(1)

L'image A₁B₁ sert d'objet pour la seconde lentille ; celle -ci donne une image définitive A'B' telle que : C₂ = 1/OA'-1/OA₁.(2)

(1) + (2) donne : C₁ + C₂ =1/OA'-1/OA. avec C_ass = 1/OA'-1/OA

Pour deux lentilles L' identiques accolées : 2C' = C=10 soit C' = 5,0 d..

Une lentille L' seule donne d'un objet AB situé 30 cm à sa gauche, une image A'B' située à 90 cm de A à droite de l'objet.

Calcul de la distance focale f' :

1/f' = 1/OA'-1/OA avec OA = -0,3 m ; OA' =0,6 m

1/f' = 1/0,6 +1/0,3 = 3/0,6 = 5,0 d. f' = 1/5 = 0,2 m.

La lentille L est utilisée seule. On place l'objet ( le même qu'en I.) 5 cm à sa gauche.

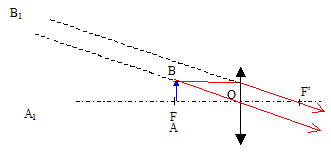
Caractéristiques de l'image : droite, virtuelle ( située à gauche de la lentille). B₁est obtenue à l'intersection des prolongements des rayons lumineux.

Par le calcul :

1/f' = 1/OA₁-1/OA avec OA = -0,05 m ; 1/f' = 10 d.

1/OA₁ =1/f' +1/OA =10+1/--0,05) = -10 ; OA₁ =-0,10 m ( à gauche de la lentille)

grandissement : OA₁/ OA = -0,1 / (-0,05) = 2 ( image droite).

L'objet AB est en réalité une pièce de monaie.

Diamètre de cette pièce ( en mm ) sachant que l'image que donne la lentille de cette pièce a une surface de 12 cm² :

Le diamètre de l'image est deux fois plus grand que le diamètre réel de la pièce.

Or la surface est proportionnelle au carré du diamètre : la surface de la pièce est donc : 12/4 = 3 cm².

surface = pD²/4 ; D² = 4S/p = 12 / 3,14 voisin de 4 soit D voisin de 2 cm ou 20 mm.

On souhaite prolonger la vision de A₁B₁ sans fatigue pour l'oeil. A₁B₁ doit se trouver à l'infini et AB au foyer objet de la lentille.

Déplacer la lentille de 5 cm en s'éloignant de l'objet.

retour -menu