Concours Kiné : tension aux bornes d'une bobine inductive 2007 ( Ceerrf)

Question 1 : 12 pts/40 sans calculatrice

---

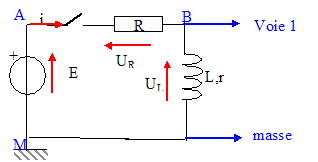
Equation différentielle à laquelle obéit l'intensité du courant à la fermeture du circuit :

additivité des tensions : E= u_L+U_R.

u_L =Ldi/dt + ri et u_R+ R i

d'où E=Ldi/dt +(R+r) i soit di/dt + (R+r)/L i = E/L.(1)

Expressions de A, B et t en fonction de E, L, r et R :

La solution est de la forme i(t) = A+Bexp(-t/t) ; di/dt = -B/t exp(-t/t).

repport dans (1) : -B/t exp(-t/t)+(R+r)/L A + (R+r)/LBexp(-t/t) = E/L

égalité vérifiée quel que soit t si : -B/t + (R+r)/LB=0 soit t = L/(R+r).

t est la constante de temps du circuit RL ; au dela de 5t le régime permanent est établi.

égalité vérifiée quel que soit t si : (R+r)/L A =E/L soit A = E/(R+r).

à t=0, l'intensité est nulle d'où : 0 = A+B soit B=-A ; B=- E/(R+r).

i(t) = E/(R+r)(1-exp(-t/t)).

La tension u_L aux bornes de la bobine est de la forme u_L(t) = a+bexp(-t/t).

Expressions de a et b en fonction de E, R et r :

di/dt = E/(R+r) (1/t) exp(-t/t)= E/Lexp(-t/t)

u_L =Ldi/dt + ri = Eexp(-t/t) + rE/(R+r)(1-exp(-t/t)).

u_L =E (1-r/(r+R))exp(-t/t)+ rE/(R+r)

u_L =E/(r+R) [r+Rexp(-t/t)]

d'où a = rE/(r+R) ; b = RE/(r+R).
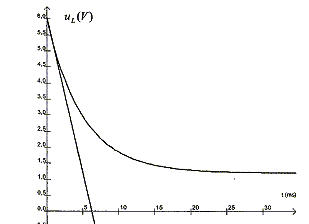
Expression de u_L en régime permanent :

à t infini : exp(-t/t) =0 et u_L =rE/(r+R) = 10*6/50 = 1,2 V.

On retrouve cette valeur sur la courbe :

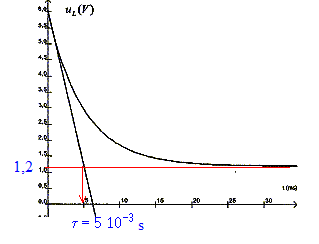
Equation de la tangente à la courbe u_L(t) à l'origine: u_L =E/(r+R) [r+Rexp(-t/t)]

coefficient directeur :[du_L/dt]_t=0 = RE/(r+R)(-1/t);

La tangente passe par le point (0 ; E) d'où son équation u = RE/(r+R)(-1/t) t +E

Lorsque u = rE/(r+R) alors 1 - r/(r+R)= R/(r+R)(1/t) t

R = R(1/t) t soit t = t

Détermination graphique de la constante t : abscisse de l'intersection de la tangente à l'origine avec l'asymptote horizontale

Le graphe indique t = 5 10^-3 s.

Valeur de L :

t = 5 10^-3 = L/(R+r) = L/50 soit L= 0,25 H.