Aurélie 04/06/07
 

concours électroradiologie médicale champ magnétique et forces électromagnétiques, ondes sur une corde. Caen 2007

Google

 

Cmposante horizontale du champ magnétique terrestre : Bh = 2 10-5 T ; perméabilité du vide m0 = 4p 10-7 u S.I.

N'ayant pas le document annexe, les schémas ont été imaginés à partir du texte.

A. étude de champs magnétiques.

  1. On a représenté le spectre magnétique d'un aimant droit :
    - Indiquer le pôole nord et le pôle sud de l'aimant. Justifier.
    - Représenter en O et en P le vecteur champ magnétique.
  2. A l'aide d'une boussole on a repéré la direction du champ magnétique terrestre en un lieu donné. Selon une direction perpendiculaire à celle du pôle nord magnétique, on approche de la boussole l'aimant droit. L'aiguille de la boussole tourne d'un angle q= 68 vers l'est.

    - Représenter le vecteur correspondant à la composante horizontale du champ magnétique terrestre, le vecteur champ magnétique de l'aimant et le vecteur champ magnétique résultant.
    - Exprimer puis calculer la valeur du champ magnétique crée par l'aimant.
    - Exprimer puis calculer la valeur du champ magnétique résultant.

  3. On veut reproduire au centre d'un solénoïde de longueur L = 50 cm, un champ magnétique Bsolénoide = 250 Bh, l'intensité du courant est I = 2,0 A.
    - Exprimer la valeur du champ magnétique au centre du solénoïde de longueur L comportant N spires et parcouru par le courant I.
    - Quelle est la valeur de N pour obtenir Bsolénoide = 250 Bh.
B. forces électromagnétiques :

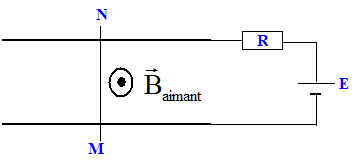
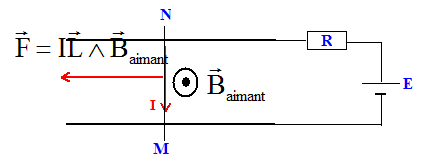
Le schéma représente en vue de dessus l'expérience des rails de Laplace. Le générateur a une fem E =6,0 V et une résistance interne R=0,30 ohm. La barre mobile MN, de résistance négligeable ferme le circuit entre le deux rails. Elle est placée dans l'entrefer d'un aimanr en U de largeur d= 40 mm, centré sur la barre, où règne un chmp magnétique uniforme de valeur B= 1,25 10-2 T.

  1. Indiquer le sens du courant dans la tige MN.
    - Déterminer l'intensité I.
  2. Représenter la force de laplace appliquée à la tige MN et calculer sa valeur.
    - Calculer le travail de cette force pour un déplacement L= 5,0 cm de la tige.
    - Que se passe t-il si on inverse les branchements aux bornes du générateur ?
C. Ondes sur une corde :

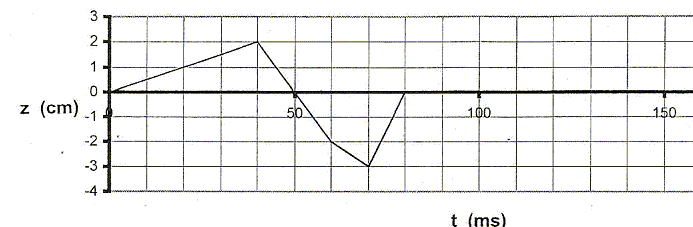
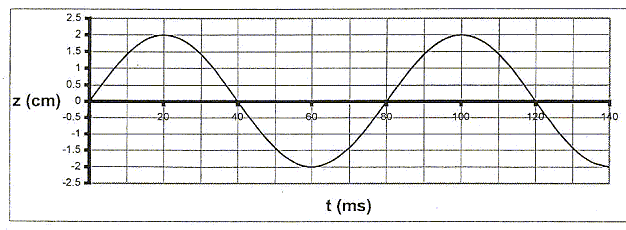
L'extrémité A d'une corde horizontale, initialement au repos, est perturbée verticalement. Cette extrémité A est choisie comme origine des abscisses. on donne sur la figure la représentation graphique de l'altitude z de A mesurée par rapport à la position de repos en fonction de la date t. Cette perturbation se propage le long de la corde à la célérité V= 2,0 m/s.

- Quel est le retard q, par rapport au point A, d'un point M d'abscisse x ? A quelle date le front d'onde arrive t-il au point B d'abscisse xB= 6,0 cm ?

La perturbation du point A est maintenant entretenue : c'est une fonction sinusoïdale du temps.

- Décrire l'aspect que prend la corde.

Déterminer la période du phénomène, sa fréquence, sa longueur d'onde.

A la date t1 = 0,8 s, quelle est l'altitude du point A ? Justifier.

Comparer l'état vibratoire d'un point D d'abscisse xD= 12 cm à celui du point C d'abscisse xC= 4 cm. Justifier.

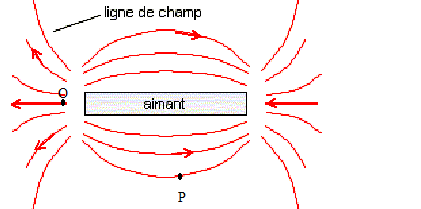
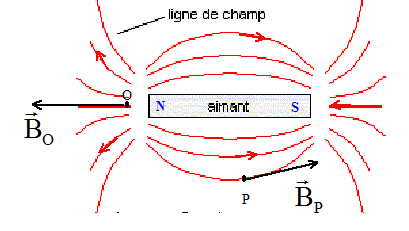
 A. Etude de champ magnétique :

A l'extérieur de l'aimant, les lignes de champ sont orientées du pôle nord vers le pôle sud ( elles rentrent au sud et sortent du nord).

Le vecteur champ magnétique est tangent à la ligne de champ, au point considéré ; ce vecteur a le sens de la ligne de champ.

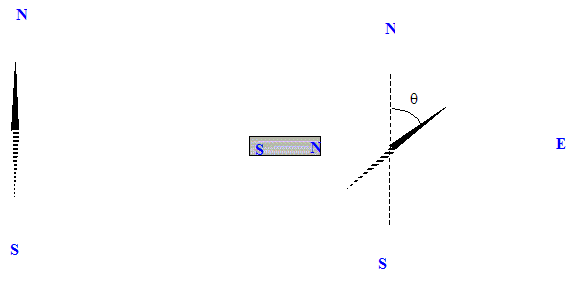
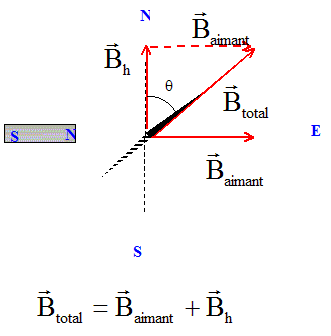
La boussole s'oriente suivant le champ magnétique total.

tan q = Baimant / Bh ; Baimant = Bh tan q = 2 10-5 * tan 68 = 5,0 10-5 T.

cos q = Bh / Btotal ; Btotal = Bh / cos q = 2 10-5 / cos 68 = 5,3 10-5 T.

Valeur du champ magnétique au centre du solénoïde de longueur L comportant N spires et parcouru par le courant I.

Bsolénoide = m0 N I / L.
Valeur de N pour obtenir Bsolénoide = 250 Bh.

N= 250 Bh L / (m0I) = 250*2 10-5 *0,5 /(4*3,14 10-7 *2) = 995 spires.

I = E/R = 6 / 0,3 = 20 A.

Le sens de la force de Laplace est donné par la règle des trois doigts de la main droite.

F= Baimant Id = 1,25 10-2 *20 * 0,04 = 0,010 N.

Travail de cette force pour un déplacement L= 5,0 cm de la tige.


W = F L = 0,01*005 = 5 10-4 J.

Si on inverse les branchements aux bornes du générateur, la tige MN se déplace dans l'autre sens.

 

Retard q, par rapport au point A, d'un point M d'abscisse x :

q = x/V = x/2 = 0,5 x.

A quelle date le front d'onde arrive t-il au point B d'abscisse xB= 6,0 cm ?

q= 0,5*0,06 = 0,03 s.

La perturbation du point A est maintenant entretenue : c'est une fonction sinusoïdale du temps.

La corde prend l'aspect d'une sinusoïde.

Période T = 80 ms = 0,08 s ; fréquence f= 1/T = 1/0,08 = 12,5 Hz ;

longueur d'onde l = VT = 2*0,08 = 0,16 m.

A la date t1 = 0,8 s, l'altitude du point A vaut :

zA(t) = 0,02 sin ( 2pt/T) = 0,02 sin (25 p t)

zA(0,8) =0,02 sin (25 p *0,8) =0,02 sin (20 p ) ; zA(0,8) = 0.

Comparer l'état vibratoire d'un point D d'abscisse xD= 12 cm à celui du point C d'abscisse xC= 4 cm.

C et D sont distants d'une demi longueur d'onde : C et D sont en opposition de phase.

retour -menu