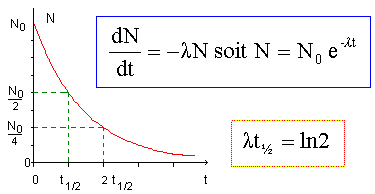Aurélie 21/03/07
 

d'après concours manipulateur électroradiologie médicale APHP 2006.

Chute verticale ; datation au carbone 14 ; défibrillateur ; savon ; conductance.

Google

Chute verticale d'un solide :

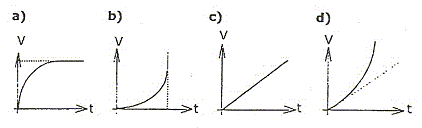
Une goutte d'eau assimilable à une sphère de rayon r, est supposée tomber dans le vide, sans vitesse initiale, à partir d'un point O choisi comme origine d'un axe Ox vertical et orienté vers le haut.

  1. L'équation horaire de sa vitesse Vx(t) est : Vx(t) = gt ; Vx(t) =- gt ; Vx(t) = [gt ]½ ; Vx(t) =- [gt ]½ ;
  2. L'équation horaire de sa trajectoire x(t) est : x(t) = ½gt2 ; x(t) =-Vt ; x(t) = gt ; x(t) = -½gt2 ;
  3. En fait la goutte d'eau tombe dans l'air de masse volumique r. La poussée d'Archimède sur cette goutte est :
    - Une poussée exercée par la goutte d'eau. Faux ( action exercée par l'air sur la goutte).
    - Le poids du volume d'eau déplacé. Faux. ( poids du volume de fluide, l'air, déplacé)
    - Une poussée verticale vers le haut. Exact.
    - Une force de valeur F= r 3pr3/4. Faux ( r g 4/3pr3).
  4. L'air produit un frottement sur la goutte. Ce frottement, de type fluide, est proportionnel à la vitesse V au carré, de même direction mais de sens contraire au vecteur vitesse. Si f est le coefficient de frottement, cette force s'écrit : ( on écrit en gras et en bleu les vecteurs)
    F= -f V ; F=f V ; F= -f V V ; F= +f V V ;. L'expression F= -f V V est exacte.
  5. La poussée d'Archimède est négligeable devant la force de frottement. Ainsi le mouvement de la goutte vérifie l'équation différentielle suivante :
    dV/dt = -fV ; dV/dt = -fV2 +g ; dV/dt = -f/m V+ g ; dV/dt = -f/m V2+ g .
    Ecrire la seconde loi de Newton sur l'axe Ox, vertical, orienté vers le haut : -mg + fV2 = -m dV/dt ; dV/dt = -f/m V2+ g.
  6. La courbe correspondante à la loi de vitesse V(t) possède l'allure suivante :

    courbe a : la vitesse augmente puis tend vers une valeur limite.
    Transformations nucléaires :
Dans la nature le carbone existe sous deux formes de noyaux isotopes, 126C et 146C. Dans la haute atmosphère un neutron formé par l'action de rayons cosmiques bombarde un noyau d'azote 14 (147N) qui se transforme en carbone 14 radioactif b- avec émission d'une autre particule.

Equation de la réaction nucléaire de formation du carbone 14.

147N + 10n --> 146C + AZX

conservation de la charge : 7=6+Z d'où Z= 1

conservation du nombre de nucléons : 14+1 = 14 +A d'où A=1 ; on identifie donc X à H

Equation de la réaction nucléaire de désintégration du carbone 14.

614C --> ZAX. + -10e. (la particule b- est un électron)

conservation de la charge : 6 = Z-1 soit Z= 7 ( noyau d'azote)

conservation du nombre de nucléons : 14 = A+0 soit A=14.

temps de demi-vie du carbone 14 : t½ = 5570 ans.

Durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.

On note N0 le nombre initiaux de noyaux de carbone 14 initiaux et N le nombre de noyaux de carbone 14 présents à la date t.

N(t½) = ½N0 ; N(2t½) = 0,25N0 ; N(3t½) = 0,125N0 ; N(4t½) = 0,0625N0 ; N(5t½) = 0,031N0 .

Allure de la courbe traduisant l'évolution de N ou encore de l'activité A= lN en fonction du temps :

" Pour obtenir une quinzaine de désintégrations par minute avec un matériau récent, il faut 1 g de carbone, c'est à dire 10 g de bois, de tissu ou de cuir, 20 g de coquillage ou 200 g d'os".

Activité A ( Bq) de 200 g d'os d'un être mort récemment : nombre de désintégrations par seconde

A= 15/60 = 0,25 Bq.

Nombre de noyaux radioactifs présents dans l'échantillon : A= lN

avec l = ln2 / t½ = ln2 / (5570*365*24*3600) =3,95 10-12 s-1.

N= 0,25 / 3,95 10-12 = 6,3 1010.

Rapport N(614C ) / (612C ) dans cet échantillon :

dans 1 g de carbone il y a : 1/12 *NA = 1/12*6,02 1023 = 5,0 1022 atomes de carbone 12

N(614C ) / (612C ) = 6,3 1010 / 5,0 1022 = 1,3 10-12.
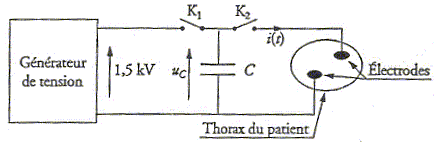
Evolution des systèmes électriques :

Le défibrillateur cardiaque est un appareil utilisé en médecine d'urgence. Il permet d'appliquer un choc électrique sur le thorax d'un patient, dont les fibres musculaires du coeur se contractent de façon désordonnée ( fibrillation). Il peut être schématisé par :

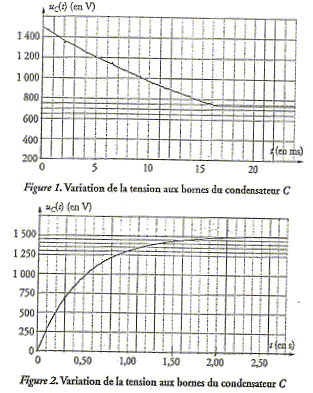
C= 470 mF ; le thorax du patient est assimilé à un conducteur ohmique de résistance R= 50 W.

Phase 1 :

Lors de la mise en fonction du défibrillateur, le manipulateur obtient la charge du condensateur C, initialement déchargé, en fermant l'interrupteur K1 ( K2 étant ouvert). Parmi les figures suivantes, quelle est celle correspondant à cette phase ? Justifier.

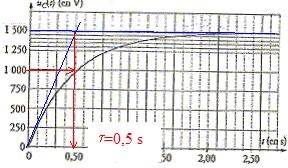
La figure 2 correspond à la charge du condensateur : la tension aux bornes du condensateur est nulle à t=0, puis est croissante ; enfin elle tend vers une valeur égale à la tension aux bornes du générateur.

Détermination graphique de la constante de temps :

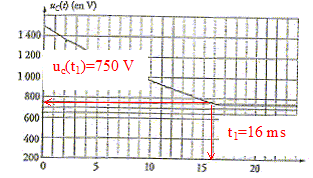
Abscisse de l'intersection de la tangente à l'origine avec l'asymptote horizontale

Ou bien, à t = t, la tension aux bornes du condensateur vaut 0,63 fois la valeur maximale soit 1500*0,63 voisin de 1000 V : noter l'abscisse correspondante.

Energie maximale stockée par le condensateur : W = ½C U2max.

W= 0,5 * 4,7 10-4 * 15002 = 529 J.

phase 2 :

Dès que le condensateur est chargé, le manipulateur peut envoyer le choc électrique en connectant le condensateur aux électrodes posées sur le thorax du patient. Il choisit alors le niveau d'énergie du choc électrique qui sera administré au patient, par exemple 400 J. A la date initiale t=0, le manipulateur ferme l'interrupteur K2 ( K1 ouvert) ce qui provoque la décharge partielle du condensateur ; la décharge est automatiquement arrêtée dès que l'énergie choisie a été délivrée.

Au cours de l'application du choc électriqu, la tension aux bornes du condensateur varie suivant uc(t) = A exp(-t/(RC)).

A est la tension maximale aux bornes du condensateur chargé : A = 1500 V.

La constante de temps vaut RC= 50*4,7 10-4 =2,35 10-2 s.

Relation liant l'intensité du courant i(t) et la charge électrique q(t) de l'armature positive du condensateur : i(t) = - dq/dt.

Relation entre la tension uc(t) et la charge électrique q(t) : q(t) = Cuc(t).

Expression de i(t) : i(t) = - dq/dt = - Cduc(t) /dt = -C(-1/(RC) A exp(-t/(RC))

i(t) = A/Rexp(-t/(RC)) ; de la forme i(t) = Bexp(-t/(RC)) avec B= A/R = 1500/50 = 30 A, valeur indépendante de C.

L'intensité est maximale à l'instant t=0.

phase 3 :

La décharge cesse dès que l'énergie W=400 J a été délivrée.

En utilisant l'une des figures ci-dessus, donner la date t1 à laquelle la décharge partielle du condensateur a été arrêtée.

En s'appuyant sur la variation de l'énergie du condensateur entre les dates t=0 et t1, on peut retrouver uc(t1)

W(t=0 ) = 529 J ; Wt1 = ½Cu2c(t1) ; W(t=0 ) -Wt1 = 400 J

529- ½Cu2c(t1) =400 ; ½Cu2c(t1) = 129 ;

u2c(t1) = 2*129/4,7 10-4 = 5,49 105 ; uc(t1) = 741 V.

Savon :

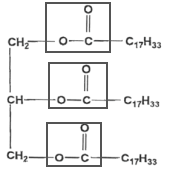
On trouve dans le commerce des savons fabriqués à partir d'huile d'olive. Ils sont obtenus en faisant réagir de la soude avec l'huile d'olive dans certaines conditions. On peut considérée que l'oléine, triester du glycérol CH2OH-CHOH-CH2OH et de l'acide oléique (C17H33-COOH) est le seul corps gras présent dans cette huile.

La molécule d'oléine, écrite ci-dessous compte trois fonctions ester.

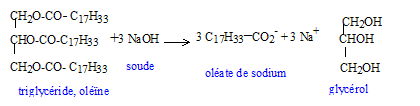
Equation de la réaction modélisant la transformation ( saponification)

On chauffe pendant 30 min un mélange de 0,10 mol d'oléine et de 0,50 mol de soude, 2 mL d'éthanol et quelques grains de pierre ponce.

Tableau d'avancement :
avancement (mol)
oléine
+ 3 NaOH
= 3 savon
+glycérol
initial
0
0,1
0,5
0
0
en cours
x
0,1-x
0,5-3x
3x
x
fin
xmax
0,1-xmax
0,5-3xmax
3xmax
xmax
si oléine en défaut : 0,1-xmax =0 soit xmax =0,1 mol (réactif limitant).

si la soude est en défaut : 0,5-3xmax = 0 soit xmax =0,17 mol

Quantité de matière de savon : 0,3 mol ; m(savon) = 304 g/mol ; masse de savon = nM= 0,3*304 = 91 g.

On représente l'ion oléate sous la forme suivante : ---------------O :

La partie hydrophile est -COO- représentée par O ; la partie hydrophobe est la longue chaine carbonée représentée par ------------

Equation entre l'ion carboxylate et l'eau :

couples acide base : RCOOH / R-COO- et H2O/HO- :

R-COO- + H2O = RCOOH + HO- ( présence majoritaire des bases R-COO- et de HO- en solution ; le pH d'une eau savonneuse est donc supérieure à 7 ).

Conductance :

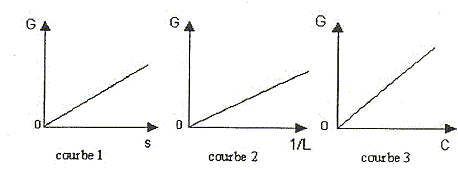
Une étude de l'évolution de la conductance G d'une solution ionique diluée en fonction des facteurs s, L, c dans les mêmes conditions de température et de pression, donne les courbes suivantes :

Que représentent C, s, L et G ? Indiquer les unités :

C : concentration de la solution en mol m-3.

s : surface (m2) des deux plaques parallèles constituant la sonde de mesure.

L : distance (m) de ces deux plaques.

G : conductance ( siemens (S)) de la portion de solution comprise entre les deux plaques.

D'après ces courbes G est proportionnelle à C, s et 1/L : G=L sC/L avec L une constante.

L = GL/(sC) ; L s'exprime en S m /(m2 mol m-3) soit en S m 2 mol-1 ;

L est une conductivité molaire ionique.

On relève les conductances obtenues dans des conditions expérimentales identiques, de solutions ioniques de concentration :
soluté
KOH
NaOH
NaNO3
G(S)
2,78 10-3
2,54 10-3
1,25 10-3
Déduire la conductance d'une solution aqueuse de nitrate de potassium KNO3 de même concentration molaire et mesurée dans les mêmes conditions.

KOH : conductivité s1 =( lK+ +lOH- ) C ; conductance G1 = ks1 = k( lK+ +lOH- ) C (1) avec k une constante.

NaOH : conductivité s2 =( lNa+ +lOH- ) C ; conductance G2 = ks2 = k( lNa+ +lOH- ) C (2)

NaNO3 : conductivité s3 =( lNa+ +lNO3- ) C ; conductance G3 = ks3 = k( lNa+ +lNO3- ) C (3)

KNO3 : conductivité s4 =( lK+ +lNO3- ) C ; conductance G4 = ks4 = k( lK+ +lNO3- ) C (4)

(4) = (1) - (2) +(3) ; G4 = G1- G2 + G3 =(2,78-2,54+1,25) 10-3 =1,49 10-3 S.
 

retour -menu