|
concours kiné APHP
radioactivité
; ondes mécaniques ; lumière
2007
|
|||
|
|||
|
masse électron m(e) = 0,0005 u; masse du proton m(p) = 1,0070 u ; masse du neutron m(n) = 1,0087 u. L'énergie de liaison moyenne par nucléon pour le noyau d'hélium 4He est 7MeV/nucléon. On admet que l'énergie de liaison associée à 1 u est de l'ordre de 1000 MeV. On admet que la fusion de trois nouaux d'hélium en un noyau de carbone expliquerait l'abondance du nucléide 12C.
La masse des électrons (6*0,0005 = 0,003 u) est négligeable devant la masse des nucléons. Le défaut de masse du noyau de carbone est Dm =0,0942 u. Faux. Dm = m(12C)-6 m(p) - 6m(n) Dm =12-6(1,0070+1,0087) = -0,0942 u. L'énergie de liaison du noyau de carbone est de 150 MeV. Faux. Energie correspondant à 0,0942 MeV : E= 0,0942*1000 = 94,2 MeV. L'énergie libérée au cours de cette fusion est de l'ordre de 13 MeV. Faux. 3 42He = 126C. Energie libérée = Energie de liaison du noyau 126C-3 Energie de liaison du noyau 42He Energie de liaison du noyau 42He : 4*7 = 28 MeV. E= 94,2-3*28 = -10,2 MeV.
23892U ---> 20682Pb + xa + yb-. Le nombre de particules b- est y=2 : Faux. 23892U ---> 20682Pb + x42He + y0-1e. Conservation du nombre de nucléons : 238 =206 +4x ; x=8. Conservation de la charge : 92 = 82 +8*2 -y ; y=6. Le nombre de particules a est x=8 : Vrai.
La loi de décroissance du nombre de noyaux N(t) de noyaux radioactifs d'un échantillon de cet uranium est N(t) = N0 exp(at) où a représente la constante radioactive et N0 le nombre de noyaux présents à la date t=0. Faux. N(t) = N0 exp(-at) La demi vie de cet échantillon est la durée au bout de laquelle son activité est divisée par deux : Faux. Il faudrait préciser " activité initiale " pour que ce soit vrai.
L'onde qui se propage à la surface de l'eau est une onde longitudinale. Faux. La déformation du milieu est verticale tandis que l'onde se propage suivant une horizontale : donc onde transversale. La célérité de l'onde a pour valeur 2 m/s. Faux. Célérité (m/s) = distance (m) / durée (s) = 1/2 = 0,5 m/s. Le bouchon possède de l'énergie mécanique. Vrai. Le bouchon se déplace suivant la verticale lors du passage de l'onde. L'énergie potentielle de pesanteur et l'énergie cinétique du bouchon varient. Le bouchon A se rapprochera du bouchon B. Faux. Les deux bouchons se déplacent suivant deux verticales : l'onde ne transporte pas de matière, mais de l'énergie.
Une lampe à vapeur de sodium émet un rayonnement de fréquence n =5,099 1014 Hz. Dans l'air, la couleur de ce rayonnement est jaune. La célérité de la lumière dans le vide est c= 3 108 m/s. On donne : 5,099*589 = 3000 ; 589/1,33 = 443. La longueur d'onde de ce rayonnement est 589 nm. Vrai. n = c/l ; l= c/n ; l= 3 108 / 5,099 1014 =3000 / 5,099 105 / 1014 =589 10-9 = 589 nm. Le rayonnement pénètre dans l'eau, d'indice de réfraction 1,33 donc la longueur d'onde du rayonnement dans ce milieu est 443 nm. Vrai. n= célérité de l'onde dans le vide / célérité de l'onde dans le milieu. n = c/v. l= c/n ; la fréquence est une caractéristique de l'onde indépendante du milieu de propagation. l0= c/n ; l= v/n = c / (nn ) ; l= l0/ n. l= 589 / 1,33 = 443 nm. Célérité (m/s) = distance (m) / durée (s) = 1/2 = 0,5 m/s. Dans l'eau la longueur d'onde du rayonnement est voisine de celle de l'ultra-violet. Faux. La limite entre le violet et l'ultra-violet, dans le vide est 400 nm. Il faudrair écrire " est voisine de la longueur d'onde de l'ultra-violet dans le vide" pour être vrai. Si une telle lumière traverse une fente fine de diamètre a= 0,3 mm, la lumière est diffractée. Sur un écran situé à D= 3 m la largeur de la tache est L= 0,443 mm. Faux.
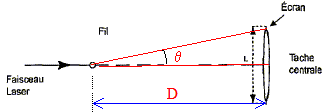
tan q = ½L/D voisin de q radian pour les angles petits. d'autre part q = l/a. avec : l longueur d'onde (m) et a : largeur de la fente (m) L= 2 lD/a = 2*589 10-9 *3 / 3 10-4 =2*589 10-5 ; L =1,2 10-2 = 12 mm. ( 0,0118 m)
|
|||
|
|
|||
|
|