Aurélie 18/09/07
 

mathématiques ; électricité ; levier concours contrôleur affaires maritimes 2006 interne

Google

Une entreprise veur conditionner ses soupes de poissons dans des boîtes de conserve ayant la forme d'un cylindre de révolution et de surface S donnée ( surface latérale + surface du fond + surface du couvercle ). On note h la hauteur de la boîte et R le rayon de la base. L'unité de longueur est le centimètre.
  1. Exprimer le volume V de la boîte en fonction de R et S.
    On impose désormais que la surface de la boîte soit égale à S=150 p.
  2. Soit la fonction définie sur [0 ; 8] par V(x) = 75p x-px3.
    - Calculer V'(x) et étudier son signe.
    - Dresser le tableau de variation de V sur [0 ; 8 ]
  3. Déterminer R pour que le volume de la boîte soit maximum.
    - Quel est alors le volume de la boîte et sa hauteur.
    réponse :

    Volume de la boîte V = section * hauteur = V= p R2 h.
Or S= surface latérale + surface du fond + surface du couvercle = 2 pR h + p R2 + p R2 ;

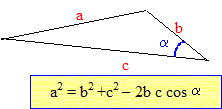
S= 2 pR h + 2 p R2 donne : h = (S-2 p R2 ) / 2 pR

V= p R2 h. s'écrit : V= ½ R (S-2 p R2 ).

Si S=150 p le volume V s'écrit : V= ½R ( 150p -2pR2)

V = 75pR-pR3.

La dérivée V'(x) s'écrit : V'(x) = 75p - 3px2.

V'(x) = 0 si 75p - 3px2 = 0 ; 25 = x2 ; x = +5 et x = -5, (valeur exclue sur l'intervalle d'étude ).

La dérivée est positive sur [ 0 ; +5 ]
x
0

5

8
V'
positive
0
négative
V
0 .....................croissante
250 p
décroissante................88 p
Le volume de la boîte est maximum si R = 5 cm.
V= 250 * 3,14 = 785 cm3.

 hauteur : V/ ( pR2 ) = 250 / 25 = 10 cm.
Soit un triangle ABC avec AB= c, AC=b, BC=a, et l'angle (AB, AC)= a. Exprimer a2 en fonction de b, c et a.

réponse :

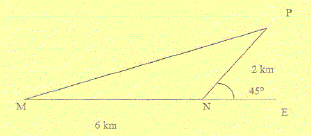
Une vedette partant d'un point M va intercepter un bateau en N à 6 km vers l'est puis va à 2 km vers le nord est récupérer un colis jeté à l'eau en P et ensuite revient directement en M. Que vaut la distance PM ?

On donnera la valeur exacte puis la valeur arrondie à 0,01 km près.

réponse :

PM2 = MN2 + NP2 - 2MN*NP cos 135

cos 135 = -0,5* racine carrée (2) = -0,5*2½

PM2 =36 + 4-2*6*2 (-0,5*2½)

PM2 =40+12*2½ ; PM= [40+12*2½]½

PM= [40 * 12*1,414]½ = 56,968½ =7,55 km.

 
 
Electricité :

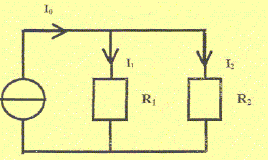
Soit le circuit représenté ci-dessous :
En appliquant la loi des noeuds, donner la relation liant I0, I1, I2.

Soit U la tension aux bornes de R1 et/ou R2. Appliquer la loi d'Ohm à R1 puis à R2 et exprimer U en fonction de R1, R2 et I0.

Exprimer I1 et I2 en fonction de R1, R2 et I0.

Calculer I1 et I2 si I0 = 8 A, R1 = 150 W et R2 = 50 W.

réponse :

Relation entre les intensités ( loi des noeuds) : I0= I1+ I2 (1)

Loi d'Ohm : U= R1 I1 soit I1 = U/R1.

U= R2 I2 soit I2 = U/R2.

Repport dans (1) : I0 = U [1/R1+ 1 / R2] = U(R1+R2) / (R1R2)

U= I0R1R2 / (R1+R2).

I1 = U/R1 = I0R2 / (R1+R2) = 8*50/200 =2 A.

I2 = U/R2 = I0R1 / (R1+R2) = 8*150/200 =6 A.

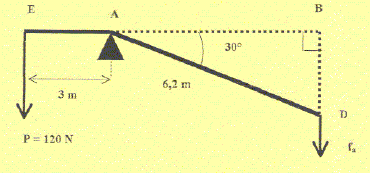
Le système suivant est constitué d'une barre rigide ED ( levier) dont le point d'appui se trouve en A. Déterminer la force verticale fa qu'il faut appliquer sur la barre rigide en D pour supporter une charge P=120 N. On ne tiendra pas compte du poids de la barre ( levier)
réponse :

Effet de rotation de P appliquée en E : P*EA = 120 * 3 = 360 Nm.

Effet de rotation de fa appliquée en D : fa AB =5,369fa

Le bras de levier est AB = AD cos 30 = 6,2*0,866 = 5,369 m

Ecrire que les deux effets de rotation des forces se neutralisent :

5,369 fa = 360 soit fa =360/5,392 = 67 N.

 
retour -menu