Aurélie 8/05/07
 

concours orthoptie Nantes mouvement d'un skieur. 2006

Google

 

Données : masse du skieur m=80 kg ; g = 9,8 m/s².

L'ensemble des forces de frottements est assimilée à une force unique, opposée au mouvement d'intensité constante F= 50 N.

Le skieur reste constamment en contact avec le sol.

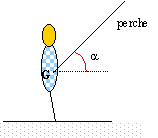
Accélération initiale :

Afin de monter au sommet de la piste, le skieur se présente sur l'aire de départ horizontale. Initialement immobile, il s'accroche àune perche faisant un angle a=45°, constant avec l'horizontale. La perche exerce une force de traction dirigée suivant sa propre direction. Après un parcours de longueur 8 m, la vitesse se stabilise à la valeur v0= 2 m/s.

  1. Démontrer que le vecteur accélération de G supposé constant a pour norme a1 = 0,25 unité S.I. Préciser l'unité.
    - Déterminer l'expression littérale puis la valeur numérique de la force constante T exercée par la perche sur le skieur.
    Montée :
  2. Le skieur toujours tiré par la perche, monte à vitesse constante (2m/s) une pente rectiligne inclinée de b=40° par rapport à l'horizontale. La perche forme un angle a=70° avec l'horizontale. ( d = 30° par rapport au plan incliné).
    - Tracer toutes les forces qui s'exercent sur le skieur et le vecteur accélération G.
    - Déterminer littérallement puis numériquement l'intensité de la force T exercée par la perche sur le skieur.
    Arrivée sur une plate forme horizontale :
  3. Le skieur arrive au sommet avec la vitesse précédente ( 2 m/s), sur une plate forme horizontale où il lâche la perche. Quelle distance aura t-il parcouru sur la plate forme ?
 

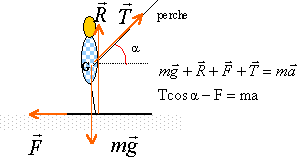
Accélération initiale :

système : le skieur et équipement; référentiel terrestre galiléen.

Ecrire la seconde loi de Newton, le skieur étant soumis à son poids, à l'action de la perche, à l'action du sol .

projeter cette relation vectorielle sur un axe horizontal à droite.

T= (ma +F)/ cosa.

calcul de l'accélération :

v0² -v² init = 2a d avec v init = 0

a = v0² / (2d) = 2² / (2*8)= 0,25 m/s².

T= (80*0,25+50) / cos45 = 99 N.

Montée :

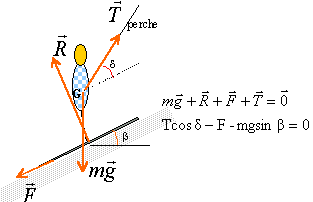
Le skieur toujours tiré par la perche, monte à vitesse constante (2m/s) une pente rectiligne inclinée de b=40° par rapport à l'horizontale. La perche forme un angle a=70° avec l'horizontale.
Schéma des forces qui s'exercent sur le skieur :

D'après le principe d'inertie la somme des forces est nulle.

projection suivant un axe parallèle au plan vers le haut

T = (F+mgsinb) / cosd.

T=(50+80*9,8*sin40) / cos30 = 639 N.

 

 

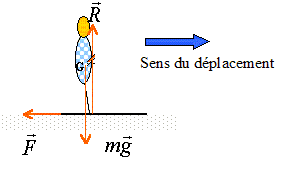
Arrivée sur une plate forme horizontale :

Le skieur arrive au sommet avec la vitesse précédente ( 2 m/s), sur une plate forme horizontale où il lâche la perche.

Distance parcourue sur la plate forme :

théorème de l'énergie cinétique ( seul fes frottements travaillent)

½ mv²fin- ½ mv²0 = -F d avec vfin= 0 ( arrêt)

Fd=½ mv²0 d'où d =½ mv²0 / F ; d= 0,5*80 * 22 / 50 = 3,2 m.
 

retour -menu