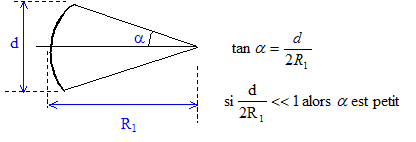Aurélie 25/04/07
 

Concours Capes : miroir sphérique, aberrations de sphéricité, lentille convergente 2007

Google

Les distances algébriques sont écrites en gras et en bleu.  
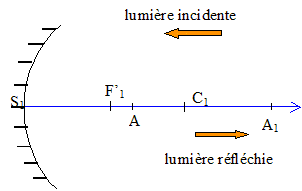
Une veilleuse est composée d'une ampoule située entre un miroir sphérique et une lentille convergente. Un dispositif muni d'un pas de vis permet le déplacement de cette lentille de façon à modifier l'angle du faisceau sortant de la veilleuse.

I Etude du miroir :

Le miroir de la veilleuse est un miroir sphérique concave de sommet S1 et de rayon de courbure R1=S1C1=5,0 cm. L'ampoule halogène sera supposée ponctuelle, en A, sur l'axe optique ; son image est A1.

  1. Rappeler la formule de conjugaison avec origine en S1 pour les points A et A1.
  2. Où devrait-on placer l'ampoule si on voulait un faisceau réfléchi parallèle.
  3. Où devrait-on placer l'ampoule si on voulait obtenir l'image de l'ampoule sur un écran situé à une distance de 1,00 m de l'ampoule.
  4. En fait l'ampoule est placée en C1 :
    - Où se trouve A1 ? Quel est l'intérêt d'un tel montage ?
  5. L'ouverture du miroir est d=4,0 cm.
    - Rappeler les conditions de Gauss.
    - Si ces conditions sont vérifiées, qu'est ce que cela impose sur le rapport d/R1 ?
    - Cette dernière condition est-elle vraie dans le cas de la veilleuse ?

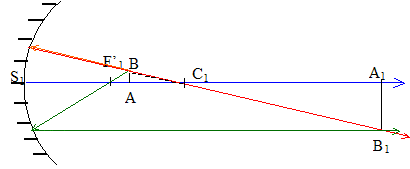
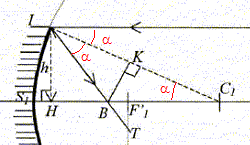
II. Etude des aberrations du miroir :

On s'intéresse à un rayon arrivant parallèlement à l'axe du miroir, en I, à une distance h=½d= 2,0 cm de l'axe. Le rayon réfléchi croise l'axe optique en B, à priori différent de F'1. T est sur ce rayon réfléchi, à la verticale de F'1.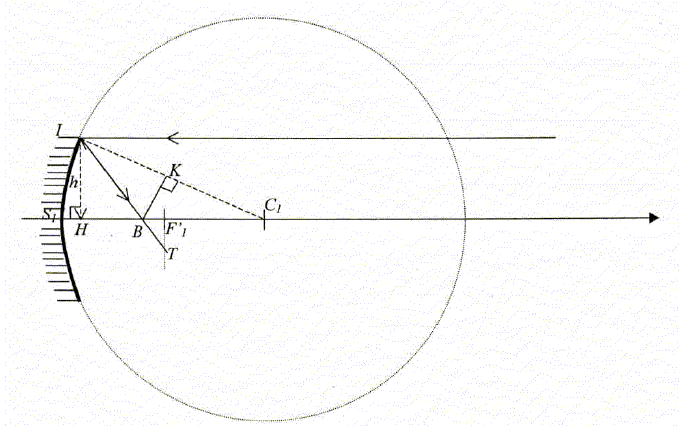

  1. Montrer que BC1=½R1[1-(h/R1)2]-½.
  2. Déterminer, en fonction de h et R1, l'aberration longitudinale de sphéricité BF'1. Calculer BF'1.
  3. Calculer numériquement l'aberration transversale de sphéricité TF'1.
  4. Conclure quand aux aberrations de sphéricité du miroir.
  5. Doit-on étudier les aberrations chromatiques pour un miroir. Justifier.

III. Etude du réglage du faisceau sortant de la veilleuse par la lentille :

L'ampoule halogène ( toujours ponctuelle, en A, sur l'axe optique )éclaire une lentille convergente mince de focale f'2=2,1 cm, de diamètre d=2h=4,0 cm, de sommet S2 placé à une distance x=AS2 de la lampe. Un pas de vis permet de déplacer cette lentille le long de l'axe optique, faisant varier x entre x1 = 1,0 cm et x2 = 2,0 cm.

  1. Faire un schéma dans le cas où x=x1, comprenant la lentille et A, ainsi que la construction de trois rayons lumineux qui aboutissent à la formation de A' image de A pour cette lentille.
  2. Définir la vergence V2 de la lentille. Donner sa valeur et préciser son unité.
  3. Déterminer S2A' en fonction de f'2 et x. Applications numériques pour x=x1 et x=x2.
  4. Dans le cas où x= 1,0 cm, faire un schéma comprenant la lentille, A, A', ainsi que le faisceau lumineux émergent issu de A et s'appuyant sur les bords de la lentille.
  5. Déterminer a, l'ouverture angulaire du faisceau de lumière émis par la lampe apès la lentille en fonction de d, f'2 et x. A.N pour x=1,0 cm et x=2,0 cm.
  6. On veut que le faisceau lumineux éclaire un livre de taille t=20 cm placé à une distance L de S2. En déduire L en fonction de t, d, f'2 et x. A.N pour x=1,0 cm et x=2,0 cm.
  7. Le livre est en fait à une distance L=1,0 m de la veilleuse. La veilleuse permet-elle de bien éclairer le livre.

IV. Etude de la diffraction due à la faible ouverture de la lentille :

On a jusqu'ici négligé la diffraction due à l'ouverture d de la lentille.

  1. Si on avait x=f'2, que vaudrait l'ouverture angulaire a0 du faisceau de lumière émis par la lampe après la lentille en négligeant la diffraction ?
  2. On prendra l=0,5 mm comme longueur d'onde de la lumière émise par l'ampoule.
  3. Calculer l'ouverture angulaire a'0 du faisceau de lumière émis par la lampe après la lentille en tenant compte de la diffraction.
  4. Comparer a0 et a'0 pour x=x1 et x=x2. Conclure.

 

Formule de conjugaison avec origine en S1 pour les points A et A1:

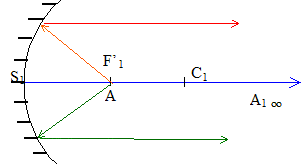
En choisissant un axe orienté dans le sens de la lumière réfléchie : 1/S1A1+1/S1A = 2/S1C1.

L'ampoule doit se trouver au foyer du miroir ( au milieu de S1C1 ),si on veut un faisceau réfléchi parallèle : l'image est alors à l'infini.

L'image de l'ampoule est sur un écran situé à une distance de 1,00 m de l'ampoule :

L'image recueillie sur un écran est réelle, située à droite du miroir.

recherche de la position de l'ampoule : AA1 = 1,00 m ; S1C1 =0,05 m

AA1 = AS1 +S1A1 =1 ; S1A1 =1-AS1 ; S1A1 =1+S1A .

La formule de conjugaison s'écrit : 1/(S1A+1)+1/S1A = 2/S1C1 =40

On pose x = S1A ; 2x+1 = 40(x2+x)

x2+0,95 x-0,025 = 0 ; S1A = 2,56 10-2 m.

L'ampoule est placée en C1 :

Calcul de  S1A1 : S1A = S1C1= -0,05 m

1/S1A1=-1/S1C1 + 2/S1C1 ; 1/S1A1=1/S1C1 ; S1A1=S1C1.

L'image de l'ampoule, placée en C1 est en C1 ; le flux lumineux de la lampe perçu par le voyageur est quasiment doublé.

Conditions de Gauss :

L'objet doit être de petites dimensions et placé au voisinage de l'axe optique ; il faut diaphragmmer pour éliminer les rayons lumineux trop inclinés sur l'axe optique.

Cette dernière condition n'est pas vérifiée dans le cas de la veilleuse : d/(2R1) = 4/10 = 0,4.
II. Etude des aberrations du miroir :

 

en I, l'angle a d'incidence est égal à l'angle de réflexion ; de plus le faisceau incident est parallèle à l'axe optique : K milieu de IC1.

Dans le triangle rectangle KBC1 : cos a = KC1/BC1 = ½R1/BC1 d'où BC1 =½R1/ cos a.

Dans le triangle rectangle IHC1 sin a = IH/IC1 = h/R1;  cos2a=1-sin2a= 1-(h/R1)2 ; cos a =[1-(h/R1)2]½.

BC1=½R1[1-(h/R1)2]-½. ( valeur : 2,728 cm)

Aberration longitudinale de sphéricité BF'1 :

BF'1 =BC1-F'1C1 = BC1-½R1 =½R1[[1-(h/R1)2]-½-1]

BF'1 =2,5[[1-(2/5)2]-½-1]=0,23 cm. (0,228 cm)

Aberration transversale de sphéricité TF'1:

TF'1 / h = BF'1 / HB avec HB = HC1-BC1 =(52-22)½-2,728 = 1,855 cm.

TF'1 = h BF'1 / HB =2*0,228 /1,855 =0,25 cm.

Conclusion : BF'1/R1 et TF'1 /R1 voisins de 0,24/5*100 = 5 %. Les aberrations de sphéricité du miroir ne sont pas négligebles.

Néanmoins cela à peu d'importance, car le but est de diriger la lumière et non pas d'otenir une image.

La réflexion est indépendante de la longueur d'onde : il n'y a pas d'aberrations chromatiques pour un miroir.

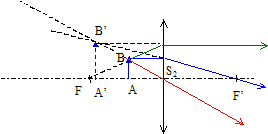
Etude du réglage du faisceau sortant de la veilleuse par la lentille :

L'ampoule halogène ( toujours ponctuelle, en A, sur l'axe optique )éclaire une lentille convergente mince de focale f'2=2,1 cm, de diamètre d=2h=4,0 cm, de sommet S2 placé à une distance x=AS2 de la lampe. Un pas de vis permet de déplacer cette lentille le long de l'axe optique, faisant varier x entre x1 = 1,0 cm et x2 = 2,0 cm.

Schéma dans le cas où x=x1, comprenant la lentille et A, ainsi que la construction de trois rayons lumineux qui aboutissent à la formation de A' image de A pour cette lentille.

 

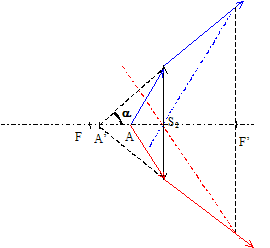
La vergence V2 de la lentille est l'inverse de sa distance focale exprimée en mètre :V2 =1/2,1 10-2 =48 dioptries = 48 d. (47,6)

S2A' en fonction de f'2 et x :

la formule de conjugaison s'écrit : 1/f'2 = 1/S2A'-1/S2A ; 1/S2A' =1/f'2 +1/S2A ; 1/S2A' =1/f'2 +1/(-x)

1/S2A' =(-f'2 +x) / (f'2 x) ; S2A' =f'2 x /(-f'2 +x).

Si x = 1 cm ; S2A' = - 2,1*1 /1,1) = 1,9 cm. (1,91 cm)

Si x = 2 cm ; S2A' = - 2,1*2 /0,1) = 42 cm.

Dans le cas où x= 1,0 cm, schéma comprenant la lentille, A, A', ainsi que le faisceau lumineux émergent issu de A et s'appuyant sur les bords de la lentille.

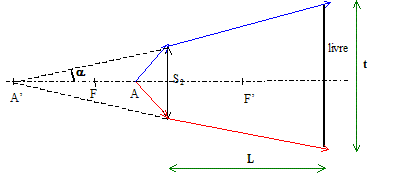
Ouverture angulaire 2a du faisceau de lumière émis par la lampe apès la lentille en fonction de d, f'2 et x.

tan a =½d/S2A' avec S2A'= f'2 x /(-f'2 +x) ; tan a =½d(-f'2 +x)/ (f'2 x).

A.N pour x=1,0 cm : tan a = 2,0/1,91 =1,047 ; a=46,3 ° ; 2a = 92,6° (93°)

pour x=2,0 cm : tan a = 2,0/42 =0,0476 ; a=2,72 ° ; 2a = 5,46° (5,5°)

On veut que le faisceau lumineux éclaire un livre de taille t=20 cm placé à une distance L de S2. Expression de L en fonction de t, d, f'2 et x.

 

tan a = ½d / A'S2 = ½t / (A'S2 + L) ; (A'S2 + L) d =A'S2 t ; A'S2 (t-d) =Ld ; L =(t/d-1)A'S2

L= (t/d-1) f'2 x /(-f'2 +x).

A.N pour x=1,0 cm : L= (20/4-1)*1,91 =7,6 cm.

pour x=2,0 cm : L= (20/4-1)*42 =1,7 m. ( 1,68 m)

Le livre est en fait à une distance L=1,0 m de la veilleuse. La veilleuse permet de bien éclairer le livre. L appartient à l'intervalle [7,6 ; 168 cm]

Etude de la diffraction due à la faible ouverture de la lentille :

Si on avait x=f'2, l'ouverture angulaire a0 du faisceau de lumière émis par la lampe après la lentille, en négligeant la diffraction vaut a0 =0 : la lampe est au foyer principal image, alors le faisceau émergent est parallèle à l'axe optique principal.

Calcul de l'ouverture angulaire a'0 du faisceau de lumière émis par la lampe après la lentille en tenant compte de la diffraction :

On prendra l=0,5 mm comme longueur d'onde de la lumière émise par l'ampoule.

a'0 = l/ d = 5 10-7 / 4 10-2 = 1,2 10-5 rad.

A.N pour x=1,0 cm : 2a = 92,6° (93°), valeur très supérieure à a'0

pour x=2,0 cm : 2a = 5,46° (5,5°), valeur très supérieure à a'0

Conclusion : l'ouverture angulaire due à la diffraction est donc négligeale.

 

 

retour -menu