Concours Capes : étude d'un tube à décharge, générateur de Thévenin 2007

Aurélie 17/04/07

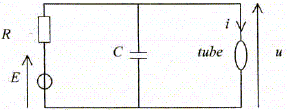
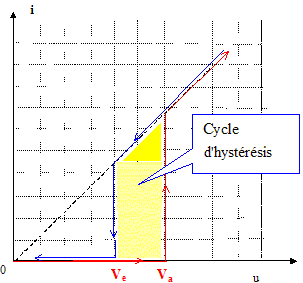
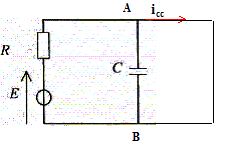
Un tube à décharge pour l'éclairage ( appelé improprement tube néon) est un dipôle électrique parcouru par un courant d'intensité i, et aux bornes duquel la tension est u, en convention récepteur. Il a deux états :
- s'il est éteint il se comporte comme un interrupteur ouvert ( l'intensité i qui le parcourt est nulle)

- s'il est allumé il se comporte comme un résistor de résistance R_a.

De plus le passage du tube vers un nouvel état dépend de l'état antérieur ( "hystérésis") :

- s'il est éteint, il faut que la tension q'il subit u devienne supérieure à la tension d'allumage V_a pour qu'il s'allume.

- s'il est allumé et que la tension qu'il subit u devient inférieure à la tension d'extinction V_e ( avec V_e <V_a) il s'éteint.

E= 150 V ; V_a = 128 V ; R= 100 kW ; C= 33,0 mF.

Tracer l'allure de la caractéristique i=f(u) du tube. On fera apparaître les effets d'hystérésis sur le graphique.
S'agit-il d'u dipôle : commandé ou libre ; linéaire ou non linéaire ; actif ou passif ?
Dans la suite du problème, on alimente le tube par un générateur de Thévenin ( de tension continue E>V_a et de résistance R) et on le branche en parallèle avec un condensateur de capacité C.
Tube éteint :
- Trouver l'équation différentielle satisfaite par u, la tension aux bornes du tube.
- Exprimer la forme de la solution u(t) en prenant u(0)=0.
Tube allumé :
- Montrer que le circuit est équivalent à un générateur de Thévenin ( de tension E' et de résistance R') qui alimente un condensateur de capacité C. On exprimera E' et R' en fonction de R, R_a et E.
- Trouver l'équation différentielle satisfaite par u, la tension aux bornes du tube.
- Exprimer la forme de la solution u(t) en prenant u(t₀)=V_a, en fonction de t, E', V_a, t₀, R' et C.
Interprétation : On suppose que R_aE/(R+R_a) >V_e.
- Décrire l'évolution de u(t) pour t >t₀.
- Tracer en justifiant, l'allure de la tension u(t) pour t>0.
- Exprimer le temps Dt qu'il faut attendre avant l'allumage de l'éclairage, en fonction de E, V_a, R et C. Calculer D t et conclure.

Allure de la caractéristique i=f(u) du tube :

Le tube allumé se comporte comme un résistor de résistance R_a : i=f(u) est alors une fonction linéaire ; la courbe est un segment de droite de coefficient directeur 1/Ra.

Le dipôle est libre ( absence de commande extérieure), linéaire seulement sur un petit intervalle, passif ( il ne peut que consommer de la puisance électrique).

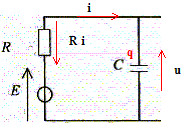
Tube éteint : le tube se comporte comme un interrupteur ouvert.
Equation différentielle satisfaite par u, la tension aux bornes du tube :

La tension aux bornes du générateur est égale à la tension aux bornes du condensateur.

u = E-R i avec i = dq/dt et q= Cu soit i = Cdu/dt

u=E-RCdu/dt ; du/dt + 1/(RC) u = E/(RC).

Solution u(t) en prenant u(0)=0 :

u(t) = E (1-exp(-t / (RC))).

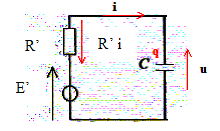
Tube allumé :
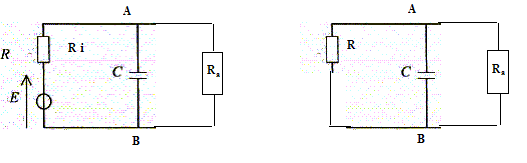
Montrons que le circuit est équivalent à un générateur de Thévenin ( de tension E' et de résistance R') qui alimente un condensateur de capacité C :

Pour calculer la résistance R' du générateur de Thévenin, on supprime E.

Entre A et B deux résistors sont en dérivation ; leur résistance équivalente vaut : R' = RR_a/(R+R_a).

Pour obtenir la fem E' du générateur de Thévenin, on cherche l'intensité de court circuit i_cc :

E-Ri_cc=0 soit i_cc = E/R.

E'= R' i_cc ; E' = ER_a/(R+R_a)
Equation différentielle satisfaite par u, la tension aux bornes du tube :

u = E'-R' i avec i = dq/dt et q= Cu soit i = Cdu/dt

u=E'-R'Cdu/dt ; du/dt + 1/(R'C) u = E'/(RC).

Solution u(t) en prenant u(t₀)=V_a :

u(t) = A exp(-t / (R'C))) + E'

V_a= A exp(-t₀ / (R'C))) + E' ; A = (V_a-E') exp(t₀ / (R'C))

u(t) =(V_a-E')exp[(t₀-t) / (R'C)] + E'

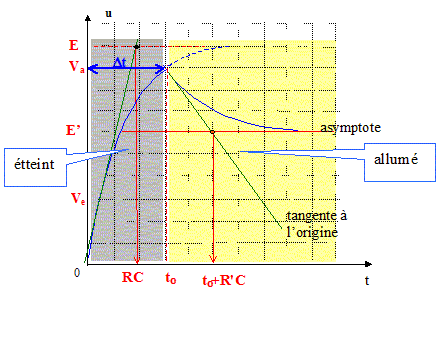
Interprétation : On suppose que R_aE/(R+R_a) >V_e.
Evolution de u(t) pour t >t₀ :

- Expression du temps Dt qu'il faut attendre avant l'allumage de l'éclairage, en fonction de E, V_a, R et C :

u(t) = E (1-exp(-t / (RC))) ( phase 1 : tube étteint)

V_a = E (1-exp(-Dt / (RC))) ; V_a / E =1-exp(-Dt / (RC)) ; exp(-Dt / (RC)) = (1-V_a / E ) = (E-V_a / E )

-Dt / (RC) = ln[ (E-V_a / E )] ; Dt = RCln[E/(E-V_a)].

Dt = 10⁵*33 10^-6 ln[150/(150-128)] = 6,3 s ( ce temps d'allumage est trop long)

retour -menu