Aurélie 11/04/07
 

Concours Capes : relèvement des virages, inclinaison du train, forme des roues 2007

Google

 

Les vecteurs sont écrits en gras et en bleu.

On s'interresse à un chemin de fer sur un sol plan horizontal, qui décrit une courbe en arc de cercle de rayon R1 pour le rail n°1, à l'intérieur de la courbe, et R2 = R1+L pour le rail n°2, à l'extérieur de la courbe, où L= 1435 mm est l'écartement des rails en Europe. On supposera que L<<R1. On suppose que les roues du train ont un rayon respectivement r1 pour la roue en contact sur le rail n°1 et r2 pour le rail n°2. Ces roues de chaque côté de la voie ferrée sont sur le même axe D et sont solidaires ; elles roulent sans glissement sur les rails.

  1. Exprimer le rapport D L2/DL1 des longueurs parcourues sur les deux rails en fonction de R2 et R1.
  2. Exprimer le rapport D L2/DL1 en fonction de r2 et r1.
  3. En déduire l'expression du rapport r2/r1 en fonction de L et R1.

Variation du rayon des roues :

  1. Montrer que dans le cas d'un chemin de fer rectiligne, les roues doivent avoir un rayon identique r1=r2=r0.
  2. Il existe donc un système qui permet de faire "varier" le rayon des roues : posons r1 = r0-d et r2 = r0+d. On supposera d<<r0.
    Effectuer un développement limité au premier ordre en     d /r0 du rapport r2/r1 ; en déduire l'expression de d en fonction de L, r0 et du rayon de courbure R1.

Inclinaison du train :

Les roues du train sont en fait des tronçons de cônes de même axe D, identiques et symétriques par rapport à l'axe du train.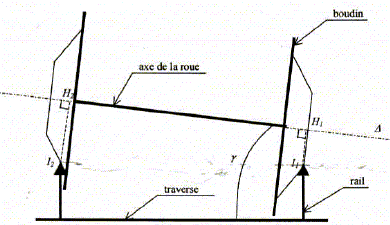

 On suppose que le plan est horizontal : la traverse est horizontale et les rails verticaux. Le point de contact du rail n°1 ( respectivement n°2) avec la roue est noté I1 ( respectivement I2) L=I1I2. H1 ( respectivement H2) est le projeté orthogonal de I1 ( respectivement I2) sur D. On a donc r1 = I1H1 et r2 = I2H2. D fait un angle g avec l'horizontale.

  1. Exprimer sin g en fonction de L, r1 et r2 puis en fonction de R1 et r0.
  2. Que vaut g dans le cas du chemin de fer rectiligne.
  3. On considère qu'une inclinaison de 2% reste tolérable pour les voyageurs. Si r0 = 1,22 m calculer le rayon de courbure minimum R1 mini.
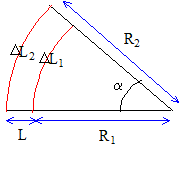
Expression du rapport D L2/DL1 des longueurs parcourues sur les deux rails en fonction de R2 et R1 :

DL1 = R1 a ( a exprimé en radian) ; DL2 = R2 a ; D L2/DL1 = R2 / R1

Expression du rapport D L2/DL1 en fonction de r2 et r1 :

Si les roues tournent d'un angle b ( radian) :

DL1 = r1 b ; DL2 = r2 b ; D L2/DL1 = r2 / r1

Expression du rapport r2/r1 en fonction de L et R1.

r2/r1 =  R2 / R1 = (L+R1) / R1 ; r2/r1 = L/R1+1.

Variation du rayon des roues :

Dans le cas d'un chemin de fer rectiligne, R1 tend vers l'infini ; en conséquence r2/r1 =1 et les roues doivent avoir un rayon identique r1=r2=r0.

On pose r1 = r0-d et r2 = r0+d. On supposera d<<r0.

r2/r1 = ( r0+d.) / ( r0-d) = (1+ d /r0) / (1- d /r0) = (1+ d /r0) (1- d /r0)-1
Effectuer un développement limité au premier ordre en d /r0 du rapport r2/r1 :

(1- d /r0)-1 = 1 +d /r0 ; r2/r1 =(1+ d /r0)2 ; r2/r1 = 1+ 2d /r0.

Expression de d en fonction de L, r0 et R1:

d'une part r2/r1 = L/R1+1 ; d'autre part r2/r1 = 1+ 2d /r0.

L/R1+1 = 1+ 2d /r0 ; L/R1 = 2d /r0 ; d = ½Lr0/R1.

Inclinaison du train :

Expression de sin g en fonction de L, r1 et r2 puis de R1 et r0.

sin g =(r2-r1)/L avec r1 = r0-d et r2 = r0+d soit r2-r1=2d

sin g = 2d /L avec d = ½Lr0/R1.

sin g = r0/R1.

Dans le cas du chemin de fer rectiligne, R1 tend vers l'infini et sin g tend vers zéro : g =0.

On considère qu'une inclinaison de 2% reste tolérable pour les voyageurs. Si r0 = 1,22 m

Calcul du rayon de courbure minimum R1 mini :

R1 mini = r0 / sin g = 1,22 / 0,02 = 61 m.

 
 

retour -menu