Aurélie 11/04/07
 

Concours Capes : étude mécanique du rotor du moteur asynchrone 2007

Google

 

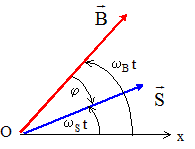
Les vecteurs sont écrits en gras et en bleu.

Le rotor du moteur asynchrone est une bobine plate, fermée sur elle même, de surface totale S=Suz, de résistance R, d'inductance L qui peut tourner autour de l'axe (Oz) passant par son centre et perpendiculaire à S. La bobine est solidaire d'un volant de grand moment d'inertie régularisant sa vitesse de rotation WS =wSuz. Le rotor du moteur asynchrone ressent le champ magnétique crée par le stator, de valeur constante B0, tournant autour de l'axe (Oz) à la vitesse angulaire constante WB =wBuz. Le retard de phase initial de la bobine sur le champ tournant est j.

L'intensité est de la forme i(t) = Imax cos(wt+j-Y) avec Imax= w B0S [R2+(Lw)2 ] -½ ; sinY =R /[R2+(Lw)2 ] -½ et w = wB-wS

  1. Donner l'expression du moment magnétique m de la bobine.
  2. Donner l'expression de la projection Gz suivant uz du couple instantané des actions électromagnétiques exercées sur la bobine, en fonction de t,Y, j, w, R, L, B0 et S.
  3. Exprimer le couple moyen C=<Gz> en fonction de w, R, L, B0 et S.
  4. Déterminer la valeur C0 du couple moyen pour wS=0. Le moteur peut-il démarrer seul ?
  5. Dans quelles conditions le couple est-il moteur ou résistant ?
  6. Exprimer la valeur maximale Cmax du couple moyen dans le cas moteur et la vitesse angulaire du rotor wS= wmax pour laquelle cette valeur est atteinte.
  7. Donner l'allure de la courbe représentant C(wS)
 

Expression du moment magnétique m de la bobine :

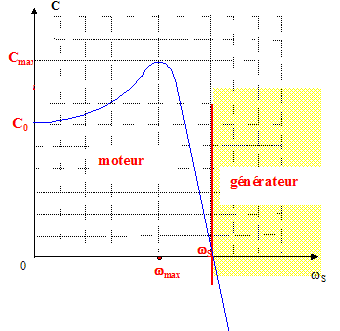
m= i (t)S.

Expression de la projection Gz suivant uz du couple instantané des actions électromagnétiques exercées sur la bobine, en fonction de t,Y, j, w, R, L, B0 et S :

G= m ^ B = i (t) S ^ B avec w = wB-wS

G= i(t) S B0 sin( w t + j) uz

Dans le plan (Oxy), représentation du champ tournant B et du vecteur surface S :

 

Or i(t) = Imax cos(wt+j-Y) avec Imax= w B0S [R2+(Lw)2 ] -½

d'où : G= w B20S2 [R2+(Lw)2 ] -½cos(wt+j-Y) sin( w t + j) uz

Expression du couple moyen C=<Gz> en fonction de w, R, L, B0 et S :

C=<Gz>=w B20S2 [R2+(Lw)2 ] -½ <cos(wt+j-Y) sin( w t + j)>

Calcul de la valeur moyenne <cos(wt+j-Y) sin( w t + j)>

Or cos(wt+j-Y) = cos((wt+j) cos Y + sin((wt+j) sin Y.

cos(wt+j-Y) sin( w t + j) = cos((wt+j)sin( w t + j) cos Y + sin2((wt+j) sin Y.

cos(wt+j-Y) sin( w t + j) =½sin[ 2( w t + j) ]cos Y + sin2((wt+j) sin Y.

La valeur moyenne <sin[ 2( w t + j) ]> est nulle.

La valeur moyenne <sin2((wt+j)> vaut ½

d'où <½sin[ 2( w t + j) ]cos Y + sin2((wt+j) sin Y>= ½sin Y =½R /[R2+(Lw)2 ] -½

C=<Gz>=w B20S2 [R2+(Lw)2 ] -½ ½R /[R2+(Lw)2 ] -½

C=½w RB20S2 [R2+(Lw)2 ] -1

Valeur C0 du couple moyen pour wS=0 :

w = wB-wS et wS=0 d'où : w = wB.

C0=½wB RB20S2 [R2+(LwB)2 ] -1

Le moteur démarre seul si le couple C0 l'emporte sur le couple résistant.

Dans quelles conditions le couple est-il moteur ou résistant ?

C est du même signe que w et w = wB-wS :

si wB>wS le couple est moteur ; si wB<wS le couple est résistant.

Expression de la valeur maximale Cmax du couple moyen dans le cas moteur :

Le couple moteur est maximal lorsque la dérivée dC/dw s'annule.

Calcul de la dérivée dC/dw avec C=A w [R2+(Lw)2 ] -1 , A= ½ RB20S2

dC/dw = A[R2+(Lw)2 ] -1 -2AL2 w2 [R2+(Lw)2 ] -2

dC/dw = A[R2+(Lw)2 ] -2 [R2+(Lw)2 -2L2 w2 ] = A[R2+(Lw)2 ] -2 [R2-(Lw)2 ]

dC/dw =0 si R2-(Lw)2 = 0 soit w = R/L ( pour le cas moteur)

Cmax=B20S2/(4L )

La vitesse angulaire du rotor wS= wmax pour laquelle cette valeur est atteinte vaut :

w = wB-wS ; wS = wB-w = wB-R/L

Allure de la courbe représentant C(wS)  

 
 

retour -menu