Aurélie 11/04/07
 

Concours Capes : alternateur triphasé 2007

Google

 

Les vecteurs sont écrits en gras et en bleu.

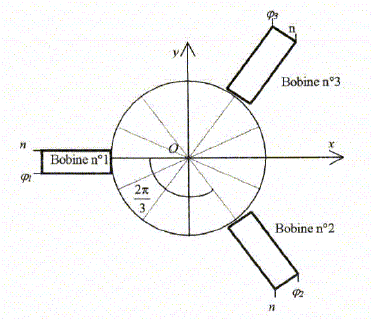
(O, ux, uy, uz) est un repère ortonormé direct.

Le stator est constitué de trois enroulements cylindriques identiques d'aire S. On repère par le vecteur surface S1=Sux la surface de la première bobine. Chacun des vecteurs Sk ( pour k= 1, 2, 3) est choisi grâce à la "règle de la main droite" à partir de l'orientation du courant Ik circulant dans la bobine n°k.

  1. Exprimer S2 et S3 dans le repère donné sans exprimer numériquement les fonctions trigonométriques.
  2. Un rotor, sur lequel se trouve un aimant permanent, tourne autour de l'axe Oz avec la vitesse angulaire W = wuz. On admet qu'il crée un champ magnétique B, de valeur B, tournant à la vitesse angulaire W . Le rotor est initialement orienté suivant Ox. Donner l'expression des composantes Bx(t) et By(t) du champ magnétique au cours du temps.
  3. Chaque bobine est constituée de N spires et a une section S. La résistance interne de chaque bobine est supposée nulle. On néglige le champ magnétique induit dans les bobines devant celui crée par le rotor. On note Uk la tension créee aux bornes de la bobine n°k en convention récepteur. On réalise un couplage en étoile, c'est à dire qu'un des pôles ( noté n, de potentiel conventionnellement nul ) est commun aux trois bobines. L'autre pôle de la bobine n°k est au potentiel Uk(t).
    - La tension aux borne de la bobine n°k est Uk(t)=RkIk-ek. Exprimer ek, en fonction de     Fk le flux magnétique que reçoit la bobine.
    - Déterminer     F1, F2, F3, les flux magnétiques reçus par chaque bobine.
    - Montrer que l'on peut mettre les trois tensions Uk(t) sous la forme Uk(t) = -Umax sin(    wt+jk).
    On exprimera Umax en fonction de N, S, B et     w ainsi que les trois phases jk.
    - Tracer sur le même graphique les trois tensions.
    - La tension efficace entre un pôle au potentiel Uk(t) et le neutre est Umono = 220 V. En déduire la valeur numérique de Umax.
    - Que vaut numériquement la tension efficace Utri entre deux pôles différents.
 

 Expressions de S2 et S3 dans le repère donné :

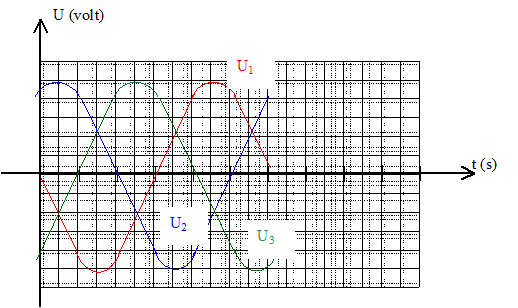
S2 = S [cos (2p/3)ux + sin (2p/3)uy ]

S3 = S [cos (4p/3)ux + sin (4p/3)uy ] = S [cos (2p/3)ux - sin (2p/3)uy ]

Expression des composantes Bx(t) et By(t) du champ magnétique au cours du temps :

Bx(t) = B cos (wt) ; By(t) = B sin (wt).

Expression de ek en fonction de Fk le flux magnétique que reçoit la bobine :

La loi de Faraday s'écrit : ek = -dFk /dt.

Flux magnétiques reçus par chaque bobine :

F1= N B.S1 =NBx(t) S = NSB cos (wt)

F2= N B.S2 =N S[ Bx(t) cos (2p/3) +By(t) sin (2p/3) ]

F2=N S B[ cos (wt) cos (2p/3) +sin (wt) sin (2p/3) ]

Or cos (wt) cos (2p/3) = ½[cos( (wt-2p/3) + cos( (wt+2p/3)]

et sin (wt) sin (2p/3) =½[cos( (wt-2p/3) - cos( (wt+2p/3)]

cos (wt) cos (2p/3) +sin (wt) sin (2p/3) = cos( (wt-2p/3)

F2=N S Bcos( (wt-2p/3).

F3= N B.S3 =N S[ Bx(t) cos (2p/3) -By(t) sin (2p/3) ]

F3=N S B[ cos (wt) cos (2p/3) -sin (wt) sin (2p/3) ]

Or cos (wt) cos (2p/3) = ½[cos( (wt-2p/3) + cos( (wt+2p/3)]

et sin (wt) sin (2p/3) =½[cos( (wt-2p/3) - cos( (wt+2p/3)]

cos (wt) cos (2p/3) -sin (wt) sin (2p/3) = cos( (wt+2p/3)

F3=N S Bcos( (wt+2p/3).

Expressions des trois tensions : Uk(t)=RkIk-ek avec ek = -dFk /dt.

F1= NSB cos (wt) ; e1 = NSBw sin (wt) ; U1(t) = R1I1-NSBw sin (wt) ; à vide I1 est nulle.

U1(t)= -NSBw sin (wt).

F2=N S Bcos( (wt-2p/3) ; e2 = NSBw sin( (wt-2p/3)

U2(t)= -NSBw sin( (wt-2p/3).

F3=N S Bcos( (wt+2p/3) ; e3 = NSBw sin( (wt+2p/3)

U3(t)= -NSBw sin( (wt+2p/3).

La tension efficace entre un pôle au potentiel Uk(t) et le neutre est Umono = 220 V. La valeur numérique de Umax est 220*2½ = 311 V.
La tension efficace Utri entre deux pôles différents ( système équilibré) vaut : 220 *3½ =381 V.

 
 

retour -menu