Oscillations électriques entretenues : oscillateur de Van de Pol Capes 2000

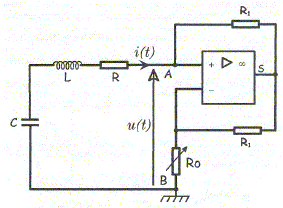
L'amplificateur utilisé est supposé idéal. En régime linéaire, sa tension de sortie est, en valeur absolue, inférieure à la tension de saturation notée V_sat.

Relation entre la tension u(t) = V_A-V_B, i(t) et R₀ :

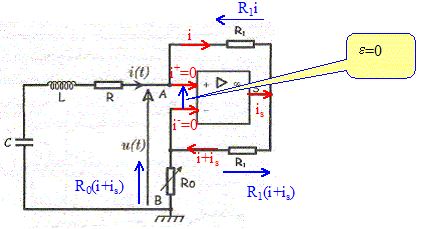
u(t) = R₀(i+i_s) ; u(t) = R₁i + (R₁+R₀)( i+i_s)

d'où R₁i +R₁( i+i_s) =0 soit i_s = -2i

Par suite : u(t) = -R₀i(t)

Valeur de R₀ conduisant à l'entretien des oscillations :

En notant v(t) la tension aux bornes du condensateur :

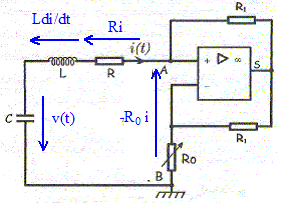
v(t) + R i(t) + Ldi(t) /dt-R₀i =0

si R = R₀ : v(t) + Ldi(t) /dt = 0 ( éq. différentielle de l'oscillateur libres non amorti)

La puissance instantanée mis en jeu dans le dipôle RLC est dissipée dans le conducteur ohmique R : p = R i²(t)

A chaque instant les alimentations de l'amplificateur opérationnel fournissent au dipôle RLC la puissance R i²(t) et compensent ainsi la puissance perdue par effet Joule.

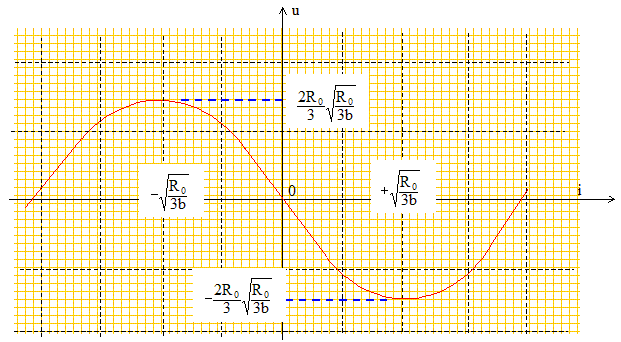
Pour tenir compte des non linéarités du montage, la caractéristique u=f(i) du dipole AB, réalisé avec l'amplificateur opérationnel, est modélisée par une courbe d'équation unique de la forme u= -R₀i + b i³.

Etude de cette fonction : u= -R₀i + b i³.

La dérivée du/di = -R₀ + 3 bi² s'annule pour les valeurs i₁ = [ R₀/(3b)]^½ et i₂ = - [ R₀/(3b)]^½

u présente donc deux extrémums pour i = i₁ et i = i₂.

La dérivée est négative sur l'intervalle [i₂ ; i₁] : la fonction u est décroissante sur cette intervalle.

La fonction u étant impaire, l'origine est centre de symétrie.

 Equation différentielle vérifiée par i(t) :

Le montage simulant une résistance négative est relié au dipôle RLC.

v(t) + R i(t) + Ldi(t) /dt+ u(t) =0 avec u= -R₀i + b i³.

dv/dt + R di/dt + Ld²i/dt² -R₀ di/dt + 3b i²di/dt= 0

Or v(t) = q/C et i = dq/dt d'où dv/dt = i/C

Par suite i/C+ (R-R₀+3 b i²) di/dt + Ld²i/dt² = 0.

i+ (R-R₀+3 b i²)C di/dt + LC d²i/dt² = 0.(1)

Condition de stabilité de cet oscillateur :

On effectue le changement de variable suivant : x= i et t = t (LC)^-½ soit dt/dt = (LC)^-½

(1) s'écrit : x + (R-R₀+3 b x²)C dx/dt + LCd²x/dt² = 0.

Or dx/dt = (LC)^-½ dx/dt et d²x/dt² = (LC)^-1 d²x/dt²

par suite : x + (R-R₀+3 bx²)(C/L)^½ dx/dt +d²x/dt² = 0.

en posant a =(R₀-R) (C/L)^½ et b=3 b / (R₀-R) :

x - a(1-bx²)dx/dt +d²x/dt² = 0.

La condition de stabilité de l'oscillateur de Van der Pol est b > ou égal à0 soit R₀> ou égal à R.