Oscillations électriques forcées, résonance d'intensité, bande passante Capes 2000

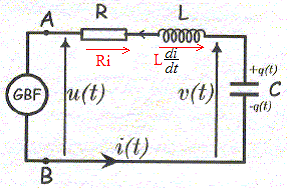
u(t) = U₀ 2^½ cos (wt) où w est la pulsation ( rad/s) et t le temps (s).

 Etude de la tension v(t) aux bornes du condensateur :

Relation entre la charge q(t) et v(t) : q(t) = C v(t).

Relation entre i(t) et q(t) : i(t) = -dq/dt.= -C dv(t) / dt.

On pose w₀ = (LC)^-½ et Q₀ = 1/R [L/C]^½.

Si R= 135 W, L=0,04 H, C= 22 nF :

w₀ = (0,04*22 10^-9)^-½ ; w₀ = 3,37 10⁴ rad/s.

Q₀ = 1/135 [0,04/22 10^-9]^½ ; Q₀ =10.

Equation différentielle vérifiée par v(t):

Additivité des tensions : v(t) = u(t)+ Ldi/dt + Ri

Or Ldi/ dt = -LC d²v/dt² = -LC v"(t)

v(t) = u(t) -LC v"(t)- RC v'(t)

v(t)= u(t) -w₀^-2 v"(t) -(Q₀w₀)^-1 v'(t)

v(t) +w₀^-2 v"(t) +(Q₀w₀)^-1 v'(t) = u(t)

Multiplier chaque terme par w₀² :

v"(t) +w₀/Q₀ v'(t)+ w₀²v(t) = w₀² u(t).

 Le GBF impose sa fréquence au dipôle AB ; celui-ci est "forcé" à osciller à la fréquence du générateur.

Le régime transitoire est de courte durée : 5 t = 5 RC = 5*135*22 10^-9 = 15 ms.

En visualisant v(t) à l'oscilloscope, on observe une sinusoïde décalée par rapport à u(t) :

v(t) = V₀ 2^½ cos (wt+ j ) avec j phase de v(t) par rapport à u(t).

On note u(t) et v(t) les nombres complexes associés aux tensions u(t) et v(t).

Expression de la fonction de transfert H(jw) = v(t) / u(t) en fonction de Q₀ et x= w /w₀ :

A la dérivée par rapport au temps correspond  la multiplication par jw.

grandeur physique	v"(t)	w0/Q0 v'(t)	w02v(t)	w02 u(t)
nombre complexe associé	(jw)2v(t) = -w2v(t)	w0/Q0 jw v(t) jww0/Q0 v(t)	w02 v(t)	w02 u(t)

L'équation différentielle s'écrit alors :

-w²v(t) + jww₀/Q₀ v(t) +w₀² v(t) = w₀² u(t)

Diviser chaque terme par w₀² et remplacer w /w₀ par x :

(-x² + jx/Q₀ +1 )v(t)= u(t)

H(jw) = v(t) / u(t) = [1-x² + jx/Q₀ ]^-1.

Multiplier numérateur et dénominateur par l'expression conjuguée : 1-x² - jx/Q₀ :

H(jw) =(1-x² - jx/Q₀) / [(1-x² )² +(x/Q₀)² ]

Expression de j :

L'argument du nombre complexe H(jw) est égal au déphasage j :

j = arctan [-x / (Q₀(1-x²)) ].

Calcul de j si w= 31500 rad/s :

x = 31500 / 3,37 10⁴ = 0,935 ; Q₀ = 10.

j = arctan[-0,935 / ( 10(1-0,935²)) = arctan (-0,740) ; j = -36,5 °.

Expression de l'impédance complexe Z du dipôle AB en fonction de R, Q₀ et x :

z = R + jLw-j/(Cw)

or w₀ = (LC)^-½ et Q₀ = 1/R [L/C]^½.

w₀Q₀ = 1/(RC) soit 1/C = Rw₀Q₀ ; w₀ / Q₀ =R/L soit L =R Q₀/ w₀.

z =R + jRQ₀w/ w₀ -jR Q₀ w₀/w ; z = R[ 1+jQ₀(x-1/x)].

module de z : Z = R [1 +Q₀²(x-1/x)² ]^½.

Valeur de Z si w = 31500 rad/s : x = 0,935 ; Q₀ = 10.

Z = 135[1+100(0,935-1/0,935)²]^½ =226 W.

L'impédance passe par une valeur minimale égale à R si x=1, c'est à dire si la pulsation du générateur est égale à la pulsation propre du dipôle RLC.

En conséquence si la valeur efficace de la tension du GBF est constante, l'intensité passe par une valeur maximale I₀ si x=1. On dit il y a résonance d'intensité.

Calcul de I₀ si U₀ = 5,4 V :

I₀ = U₀/R = 5,4 / 135 = 0,04 A.

Tension efficace V₀ aux bornes du condensateur à la résonance d'intensité :

impédance du condensateur : 1/(Cw₀) = 1/(22 10^-9 *3,37 10⁴) = 1349 W ;

V₀ = I₀ /(Cw₀) = 0,04*1349 = 54 V.

On observe une surtension ( égale à Q₀U₀) aux bornes du condensateur, à la résonance d'intensité.

La bande passante à 3 dB est l'ensemble des pulsations telles que l'intensité I soit supérieure ou égale à I₀ 2^-½.

La largeur de la bande passante est notée Dw.

Expression des pulsations de coupures, notées w₁ et w₂ :

Si I= I₀ 2^-½ alors Z = U₀/I = 2^½ U₀/ I₀ =2^½ R

Or Z = R [1 +Q₀²(x-1/x)² ]^½.

d'où 2 = 1 +Q₀²(x-1/x)²

1/ Q₀² = (x-1/x)² ; x-1/x =+1/ Q₀ et x-1/x =-1/ Q₀

x² -x/Q₀ -1 =0 ; solution positive x₂ = 0,5( 1/ Q₀ + [1/ Q₀²+4]^½) ; w₂= 0,5w₀ ( 1/ Q₀ + [1/ Q₀²+4]^½)

x² +x/Q₀ -1 =0 ; solution positive x₁ = 0,5( -1/ Q₀ + [1/ Q₀²+4]^½) ; w₁= 0,5w₀ ( 1/ Q₀ + [1/ Q₀²+4]^½)

w₂- w₁ = w₀ / Q₀.