Aurélie 27/04/07
 

Concours ca/plp externe : lentilles convergente, divergente, système afocal 2007

Google

 
Un élève se propose de faire quelques manipulations d'optique utilisant les lentilles. Pour cela il dispose :

- d'un banc d'optique horizontal

- d'un ojet réel AB tel que A appartient à l'axe optique de la lentille et AB perpendiculaire à cet axe.

- de deux supports de lentilles

- de trois lentilles minces L1 convergente de distance focale image f'1 = 100/3 cm ; L2 convergente de distance focale image f'2 inconnue ; L3 divergente de distance focale image f'3 = -20 cm.

- d'un écran perpendiculaire au banc d'optique et à l'axe optique de la lentille utilisée.

I. lentille L1 :

  1. Calculer la vergence de la lentille.
  2. Tracer le rayon émergent de la lentille correspondant à un rayon incident :
    - passant par le centre optique;
    - passant par le foyer principal objet ;
    - parallèle à l'axe optique de la lentille.
  3. La lentille L1 est placée à 50 cm de l'objet AB de hauteur h= 1 cm.
    - Déterminer la position, la nature et la taille de l'image A'B' de l'objet AB.
    - Faire la construction de l'image A'B'.
    - Si l'objet est la lettre "d" que voit-on sur l'écran ? Justifier.
  4. Sans rien modifier des positions précédentes, l'élève fait tourner la lentille et son support autour d'un axe vertical passant par le centre optique de la lentille ; il constate que l'image devient floue.
    - Quelle première condition d'obtention de bonnes images n'est pas alors respectée ?
    - Quelle est l'autre condition d'obtention de bonnes images. Comment pourrait-on vérifier expérimentalement cette condition ?
    - Comment sont appelées ces deux conditions ?
II. lentille L2 :

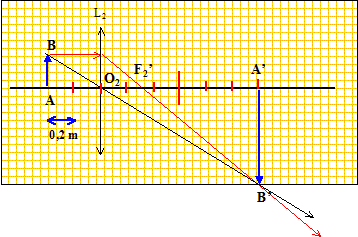
L'écran est placé à la distance D= 1,60 m de l'objet AB ; l'élève déplace la lentille jusqu'à obtenir une image réelle A'B' sur l'écran ; il constate que l'image est trois fois plus grande que l'objet. Le but est de déterminer la distance focale image f'2 de L2. 

  1. Détermination graphique :
    - Pourquoi peut-on affirmer que le centre optique O2 de la lentille appartient au segment AA' ?
    - En utilisant la figure ci-dessous, trouver la position du centre optique de la lentille et la position du foyer principal image F'2.
    - En déduire la distance focale image f'2.
  2. Détermination par le calcul :
    - A partir de la formule de grandissement, de la formule de conjugaison et de la distance AA'=D, trouver 3 relations vérifiées par O2A et O2A'.
    - En déduire la distance focale image f'2.
  3. Montrer qu'il existe une autre position de la lentille qui donne de l'objet AB une image A'B' sur l'écran situé à 1,6 m de AB. Donner alors la distance de l'objet à la lentille ainsi que le grandissement transversal. ( On peut résoudre cette question sans aucun calcul).
III. système afocal :

L'élève utilise les lentilles L1 et L3 pour réaliser un système afocal. Pour cela il place les deux lentilles de telle façon que leurs axes optiques soient confondus, la lumière traversant d'abord L3 puis L1.

  1. Qu'est ce qu'un système afocal ?
  2. Soit un rayon incident sur L3 parallèle à l'axe optique ; quelle est la direction du rayon émergent de L3 ?
  3. Le rayon émergent de L1 étant parallèle à l'axe optique, quelle est la direction du rayon incident sur L1 ?
  4. Rassembler ces résultats et tracer la marche d'un faisceau cylindrique de rayon R et dont l'axe est l'axe optique du système afocal.
  5. En déduire la distance séparant les deux lentilles.
  6. Calculer le rayon R' du faisceau émergent. A.N: R= 1 cm. Quel intérêt peut présenter un tel montage ?
  7. Montrer que ce système afocal donne d'un objet AB une image dont la taille ne dépend pas de la position de l'objet ( la réponse à cette question ne nécessite pas obligatoirement de calculs). Calculer alors le grandissement transversal g.
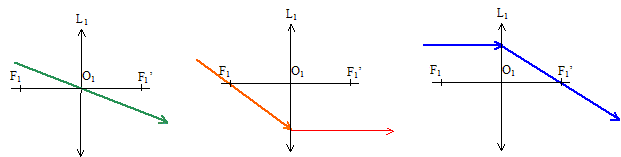
I. lentille L1 :

Vergence de la lentille : inverse de la distance focale image exprimée en m

v = 3 dioptries (3 d).

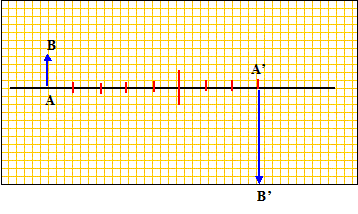
Trac des rayons émergents de la lentille correspondant à un rayon incident :

On écrit en gras et en bleu les distances algébriques.

La lentille L1 est placée à 50 cm de l'objet AB de hauteur h= 1 cm. O1A= -0,5 m

Position, nature et taille de l'image A'B' de l'objet AB :

Formule de conjugaison : 1/f'1 = 1/O1A'-1/O1A.
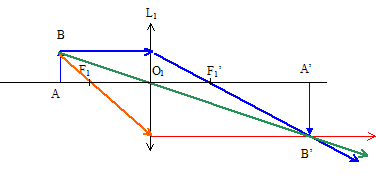
1/O1A'=1/f'1 +1/O1A = 3 +1/(-0,5) = 1 ; O1A' = 1 m.

O1A' étant positive, l'image est réelle.

grandissement transversal : g = O1A'/O1A = 1/'-0,5) = -2

image renversée de taille 2h = 2 cm.

Construction de l'image A'B' :


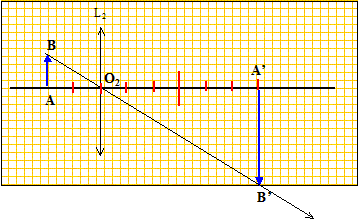
- Si l'objet est la lettre "d" sur l'écran on voit la lettre "p"

Conditions de Gauss d'obtention de bonnes images :

- objet de petites dimensions placé au voisinage de l'axe optique principal

- éliminer (utiliser un diaphragme) les rayons lumineux trop inclinés sur l'axe optique principal.

II. lentille L2 :

Détermination graphique :


Tout rayon issu de A ( respectivement de B) passant par le centre optique O2 de la lentille n'est pas dévié ; il passe donc en A' ( respectivement en B').
Position du foyer principal image F'2 :


Distance focale image f'2 = 30 cm.

Détermination par le calcul :
Grandissement transversal g = -3 = O2A'/O2A ; O2A' = -3O2A (1)

Formule de conjugaison : 1/f'2 = 1/O2A'-1/O2A (2)

Distance AA'=D = 1,6 = A O2 + O2A' ; -O2 A + O2A' =1,6 (3)

(1) et (3) donnent : -4O2A =1,6 ; O2A =-0,4 ( -0,25 D)

(1) donne : O2A' = 1,2 m (0,75 D )

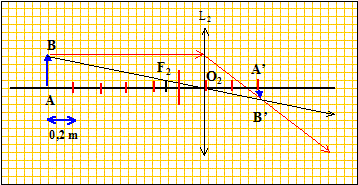
(2) donne :1/f'2 = 1/1,2 -1/(-0,4) = 0,833 + 2,5 = 3,33 ; f'2 = 1/3,33 = 0,3 m.

Il existe une autre position de la lentille qui donne de l'objet AB une image A'B' sur l'écran situé à 1,6 m de AB.

La distance de l'objet à la lentille vaut 1,2 m et le grandissement transversal vaut -1/3. 

 

III. système afocal :

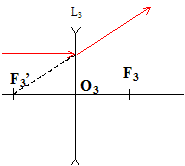
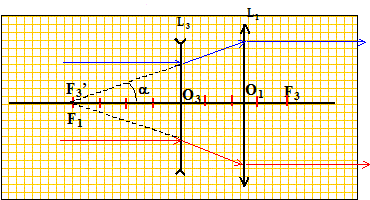
L'élève utilise les lentilles L1 et L3 pour réaliser un système afocal. Pour cela il place les deux lentilles de telle façon que leurs axes optiques soient confondus, la lumière traversant d'abord L3 puis L1.

Système afocal :

Lorsque l'image définitive est à l'infini, le système est dit afocal.

Soit un rayon incident sur L3 parallèle à l'axe optique, la direction du rayon émergent de L3 est :

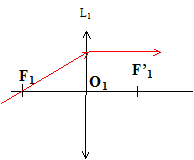
Le rayon émergent de L1 étant parallèle à l'axe optique, la direction du rayon incident sur L1 est :

Marche d'un faisceau cylindrique de rayon R et dont l'axe est l'axe optique du système afocal :

Distance séparant les deux lentilles :

Le foyer image de L3 et le foyer objet de L1 sont confondus : O3O1 = 33,3-20 = 13,3 cm.

Calcul du rayon R' du faisceau émergent si R= 1 cm :

tan a = R/F'3O3 = R'/ F1O1.

R' = R* F1O1/F'3O3 = 1*33,3/20 =1,66 cm ( 1,7 cm)

Intérêt d'un tel montage : à partir d'un faisceau cylindrique étroit, obtenir un faisceau cylindrique de même axe, mais plus large.

Grandissement transversal g :

L3 donne d'un objet AB une image intermédiaire A3B3 située en F'3 ; le grandissement est g3 = O3F'3/O3A = A3B3/AB.

A3B3 sert d'objet pour L1 ; l'image définitive A'B' est à l'infini ; le grandissement est g1 = A'B' /A3B3.

Le grandissement du système est : g =g3 g1 =A'B' /AB = R'/R = 1,7.
 

retour -menu