Aurélie 11/04/07
 

Concours Capes : propriétés et transformations d'un gaz parfait, cycle Diesel 2007

Google

 

Propriétés d'un gaz parfait :

  1. Rappeler l'équation des gaz parfaits que suit une quantité n de gaz parfait, à la pression P, dans un volume V, à la température T
  2. On note Cp et Cv les capacités thermiques respectivement à pression et à volume constants, et on rapelle l'énoncé des deux premières lois de Joule pour un gaz parfait, concernant l'énergie interne U et l'enthalpie H : dU= CvdT et dH= CpdT
    - Exprimer Cv et Cp en fonction de n, R et     g = Cp/Cv.
Equation des gaz parfait : PV=nRT

avec P : pression en pascal ; V : volume du gaz en m3 ; n : quantité de matière (mol) ; T : température ( K) ; R= 8,31 J K-1 mol-1.

Expressions de Cv et Cp en fonction de R et g = Cp/Cv :

H= U+PV = U+nRT

Différentier : dH=dU+nR dT

Or dU= CvdT et dH= CpdT d'où : CpdT = CvdT + nRdT soit : Cp = Cv +nR.

Or Cp =gCv d'où : gCv = Cv +nR ; Cv = nR / (g-1) et CP = nRg / (g-1)

Transformations d'un gaz parfait :

On supposera que le gaz n'est soumis qu'aux forces de pression. On s'intéresse à une transformation de ce gaz parfait qui le fait passer de l'état initial à la pression Pi et de volume Vi à l'état final de pression Pf et de volume Vf.

On exprimera les réponses aux questions qui suivent, uniquement en fonction de Pi , Vi, Pf , Vf, et g.

  1. Exprimer le travail WisoV échangé par le gaz lors d'une transformation isochore réversible.
  2. Exprimer le travail WisoP échangé par le gaz lors d'une transformation isobare réversible.
  3. Exprimer le transfert thermique QisoV échangé par le gaz lors d'une transformation isochore réversible.
  4. Exprimer le transfert thermique QisoP échangé par le gaz lors d'une transformation isobare réversible.
  5. Exprimer le transfert thermique QisoS échangé par le gaz lors d'une transformation adiabatique réversible.
  6. Démontrer la loi de Laplace PiVig= PfVfg que suit le gaz lors d'une transformation adiabatique réversible.
 dWisoV = -PdV = 0 car dV=0 ( isochore)
 dWisoP = -PdV ; WisoP = -P(Vf-Vi) ; P= Cte ( isobare)
DU = QisoV +WisoV = QisoV ; DU =CvDT = Cv(Tf-Ti) avec T= PV/(nR)

QisoV = Cv / (nR) [PfVf-PiVi] = 1/(g-1)[PfVf-PiVi].

DH = QisoP = CPDT = CP(Tf-Ti) avec T= PV/(nR)

QisoP = CP / (nR) [PfVf-PiVi] = g /(g-1)[PfVf-PiVi].

QisoS = 0 ( adiabatique)
Loi de Laplace :

dU= CVdT = TdS-PdV = -PdV ( adiabatique réversible donc dS=0 )

CVdT = -PdV = -nRT/V dV ; CV / (nR) d(lnT) + d(lnV) = 0 ; 1/(g-1)d(lnT) + d(lnV) =0

T1/(g-1)V= Cte ; or T=PV/(nR) d'où PVg= cte'.
 

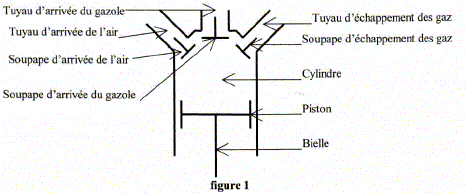
Etats thermodynamiques successifs lors du cycle Diesel :

On s'intéresse à un gaz parfait ( g=1,40)dans un cylindre de volume variable, entre Vmin=150 mL et Vmax = 400 mL, fermé par un piston, qui subit un cycle réversible dont les caractéristiques sont :

Admission : la soupape d'arrivée de l'air est ouverte ( la pression est Pmin=1,00 105 Pa, la température Tmin=300 K), les autres fermées. Le volume passe de Vmin à Vmax de façon isobare et isotherme.

Compression A--> B : les soupapes sont fermées. Le volume passe de Vmax à Vmin de façon adiabatique et réversible.

Injection B--> C : les soupapes sont fermées sauf celle d'injection du gazole. Le volume augmente jusqu'à VC=250 mL, on modélise cette phase de combustion par une évolution isobare ( P=Pmax) au cours de laquelle le gaz reçoit un transfert thermique lié à l'injection du gazole.

Détente C--> D : les soupapes sont toutes fermées. Le volume augmente encore jusqu'à Vmax mais la pression diminue. Il s'agit d'une détente adiabatique et réversible.

D-->A : ouverture de la soupape d'échappement des gaz. La pression diminue brutalement jusqu'à Pmini, le volume restant constant.

Ejection des gaz : la soupape d'échappement des gaz est ouverte, les autres fermées. Le volume passe de Vmax à Vmin de façon isobare.

  1. Déterminer numériquement ( dans les unités SI) les caractéristiques de chaque état thermodynamique intermédiaire ( pression, volume, température).
A : PA= 1,00 105 Pa ; TA= 300 K ; VA= 0,4 L = 4 10-4 m3.
A --> B adiabatique réversible : VB= 0,15 L = 1,5 10-4 m3.

PB=PA[VA/VB]g =1,00 105[0,4/1,5]1,4 ; PB= 3,95 105 Pa.

équation des gaz parfaits : TB= PBVB/(nR) avec nR = PAVA/TA.

TB= PBVBTA /(PAVA) =3,95*0,15/0,4 * 300 ; TB=4,44 102 K.

B --> C évolution isobare : PC=Pmax = 3,95 105 Pa.

VC=0,250 L= 2,5 10-4 m3.

TC= PCVC/(nR) avec nR = PAVA/TA.

TC= PCVCTA /(PAVA) =3,95*0,25/0,4 * 300 ; TC=7,41 102 K.

C --> D détente adiabatique réversible VD=Vmax=0,40 L= 4 10-4 m3.

PD=PC[VC/VD]g =3,95 105[2,5/4]1,4 ; PD= 2,04 105 Pa.

équation des gaz parfaits : TD= PDVD/(nR) avec nR = PAVA/TA.

TD= PDVDTA /(PAVA) =2,04 *0,4/0,4 * 300 ; TD=6,14 102 K.

Transformations lors du cycle Diesel :

Déterminer pour chaque phase le travail et la chaleur échangés par le gaz parfait.

A --> B adiabatique réversible : QAB=0. 

WAB= DUAB=Cv(TB-TA)= 1/(g-1)[PBVB-PAVA].

WAB=1/0,4(3,95*15-1*40)= 48,1 J.

B --> C évolution isobare : WBC = -PC(VC-VB)

WBC = -3,95 105(2,5-1,5)10-4= -39,5 J.

QBC = g /(g-1)[PCVC-PBVB].

QBC =1,4/0,4*3,95 105(2,5-1,5)10-4= 138 J.

C --> D détente adiabatique réversible QCD=0. 

WCD= DUCD=Cv(TB-TA)= 1/(g-1)[PDVD-PCVC].

WCD=1/0,4(2,04*40-3,95*25)= -42,9 J.

D --> A isochore WDA=0.

QDA = 1/(g-1)[PAVA-PDVD].

QDA =1/0,4( 1*40-2,04*40)= -104 J.

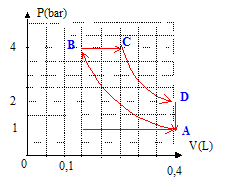
Diagramme de Clapeyron du cycle Diesel :

Exprimer numériquement la somme des travaux échangés Wtot par le gaz parfait sur un cycle. Que pensez de son signe ?

Tracer le cycle P=f(V) dans les coordonnées de Clapeyron.

Dans quel sens est parcouru le cycle Diesel dans le diagramme de Clapeyron ? Est ce normal ?

Wtot =WAB+WBC +WCD=48,1-39,5-42,9 = -34,3 J

Valeur négative, le système fonctionne en moteur ( travail fourni au milieu extérieur). Le diagramme de Clapeyron est décrit dans le sens horaire pour un fonctionnement en moteur.

Rendement du moteur Diesel :

Définir le rendement thermodynamique h et le calculer.

La vitesse maximale de rotation est N=1500 tr/min. Calculer la puissance maximale Pmax de ce moteur.

h = énergie utilisable ( travail mécanique dans ce cas )/ énergie dépensée ( énergie prélevée à la source chaude, phase BC)

h =34,3 / 138 = 0,248 ( 24,8 %)

1500 tr/min = 1500/60 = 25 tr/s, soit 25 cycles par seconde.

Chaque cycle met en jeu 34,3 J

Pmax = 34,3*25 = 857 W.
 

retour -menu