|
mécanique : moto dans un virage ; mouvements rectilignes bts MAVA 2005 et 2007 |
||||
|
||||
|
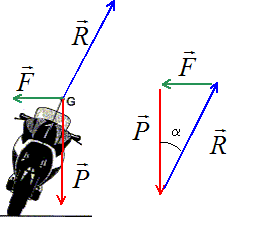
L'ensemble moto et pilote, de masse m, est animé d'un mouvement circulaire uniforme ( trajectoire circulaire horizontale de rayon r, vitesse constante V ). Les forces sont étudiées dans un repère lié à la moto. Dans ce repère, la moto étant immobile, on applique le principe de la statique au centre de gravité de la moto en ajoutant une autre force : c'est la force de repère due à l'accélération centripète de la moto. Cette force a pour intensité F= mV2/r.
Donner un autre nom pour la force de repère F. Force d'inertie centrifuge. Représenter toutes les forces extérieures et cette force de repère en les ramenant au centre de gravité G de l'ensemble ( moto et pilote).
P : poids ; R : action du sol. Donner en fonction de m et g, l'expression de la composante verticale de la réaction du sol. Ry = P= mg. Donner en fonction de m, V et r, l'expression de la composante horizontale de la réaction du sol. Rx = F= mV2/r. Soit f le coefficient de frottement entre le pneumatique et le sol. Exprimer, en fonction de g, f et r, la vitesse maximale que peut prendre la moto pour virer. f= Rx/Ry ; f = V2/ (rg ) ; V2 = g r f ; V= (g r f)½. Calculer cette vitesse
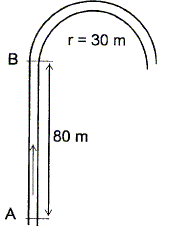
maximale pour r= 30 m, g=10 m s-2 ;
f=1,1. V=(10*30*1,1)½ = 18,16 m/s =
18 m/s. 18,16*3,6 = 65,4 km/h =
65 km/h. La moto arrive en A avec une vitesse de 140 km/h. Elle doit aborder le virage avec une vitesse maximale de 65 km/h. En utilisant la relation qui lie la vitesse, l'accélération et la distance parcourue : Vf2-Vi2= 2a(xf-xi). Calculer la décélération sur le parcours AB en la supposant constante. Vf = 65 /3,6 = 18,06 m/s ; Vi= 140 /3,6 = 38,89 m/s ; xf-xi = 80 m. a =(18,062-38,892) / 160 = -7,4 m s-2.
Le véhicule de masse 180 kg effectue un trajet rectiligne ABCDE. Il quitte le point A sans vitesse initiale et atteint le point B avec une vitesse de 90 km/h après 15 s. Au cours de cette phase le mouvement est rectiligne uniformément accéléré. Calculer l'accélération et la distance parcourue AB. accélération (m s-2)= variation de la vitesse (m s-1) / durée de cette variation (s) a = Dv/Dt avec Vf = 90/3,6 = 25 m/s et Vi=0 a = 25/15 =1,667 m s-2 = 1,7 m s-2. AB = ½at2 ; AB = 0,5*1,667*152 = 187,5 m = 1,9 101 m.
Déterminer la valeur de la force motrice sachant que sa puissance au cours de cette phase est 8,5 kW. P= F v. P ( watt) ; F( N); v (m/s) F= 8500/25 = 340 N. En déduire la valeur de la résultante des forces de frottement. Le mouvement étant rectiligne uniforme, la première loi de Newton indique que la somme vectorielle des forces est nulle. Sur une route horizontale, le poids compense l'action du sol ; la force motrice compense la force de frottement. Valeur de la force de frottement :
340
N.
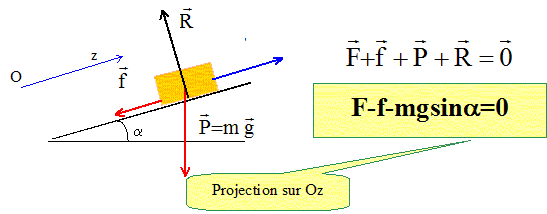
La force de frottement équivalente est parallèle à la trajectoire, de sens contraire au déplacement et de grandeur égale à 340 N. Représenter le véhicule et les forces qui s'exercent.
Déterminer la grandeur de la force motrice. g = 10 m s-2. F= f + mg sin a F= 340+180*10*0,05 = 430 N.
En déduire la puissance fournie par le moteur. P= F v. P ( watt) ; F( N); v (m/s) P= 430*25 = 10750 W = 10,75 kW
= 10,8
kW.
Calculer l'énergie cinétique en E. Ec = ½mv2 avec v = 25 m/s et m = 180 kg. Ec = 0,5*180*252 =56 250 J = 56,3 kJ. En supposant que l'énergie de freinage est totalement transformée en chaleur, déterminer l'augmentation de température des freins si ces derniers pèsent m= 1,2 kg. On donne Cp des feins =400 J kg-1 K-1. Q= mCp Dq avec Q (J) ; m(kg) ; Dq (°C) Dq = Q /(mCp) = 56250/(1,2*400) = 117 °C. |
||||
|
|
||||
|
|