Etude d'un aquarium : hydrostatique ; hydrodynamique bts enveloppe du bâtiment 2007

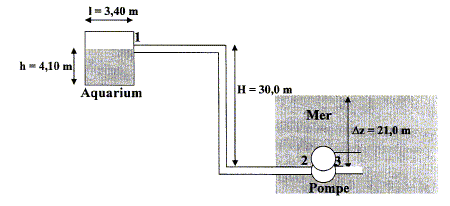
On s'intéresse à un grand aquarium situé dans un centre océanographique. Celui-ci est alimenté par de l'eau de mer grâce à un système de remplissage puisant l'eau à la profondeur Dz = 21,0 m sous le niveau de la mer et l'amenant au niveau de la surface libre de l'eau contenue dans l'aquarium sur une dénivellation totale H=30 m.

Les dimensions intérieures de l'aquarium sont : L= 8,20 m ; l = 3,40 m ; hauteur utile d'eau : h = 4,10 m.

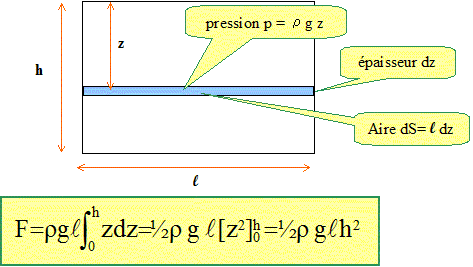
On donne : P_atm = 1,00 10⁵ Pa ; g= 9,81 m/s² ; r_eau = 1000 kg m^-3.

Débit volumique de la pompe q_v=60,0 m³ h^-1 ; diamètre intérieur de la canalisation d = 5,20 cm.

Relation de Bernoulli entre les points 1 et 2 en présence d'une machine hydraulique :

g(z₂-z₁) +½(c₂²-c₁²) +(p₂-p₁)/r =P_1-2/q_m.

Calculer la résultante des forces de pression dues à l'eau sur :

Le fond de l'aquarium :

pression exercée par l'eau sur le fond : p = rgh.

p = 1000*9,81*4,10 = 40221 = 4,02 10⁴ Pa.

Surface du fond : S= L l = 8,20*3,40 =27,88 m².

force pressante (N) = pression (Pa) * surface (m²)

F = pS = 40221 *27,88 =1,12 10⁶ N.

l'une des petites faces verticales :

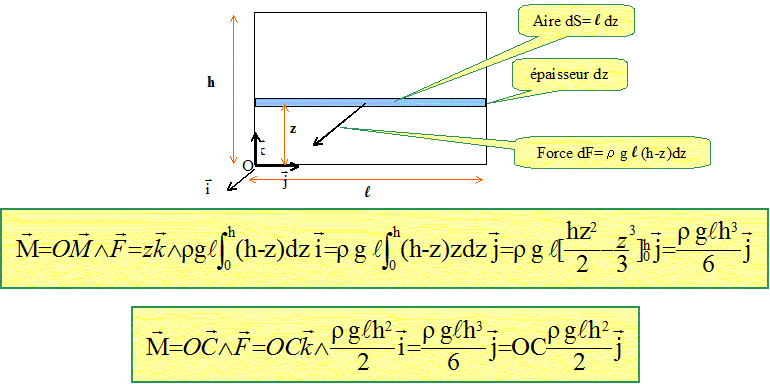
F= 0,5*1000*9,81*3,40*4,10² =2,80 10⁵ N.

l'une des grandes faces verticales :

F= ½rgLh² =0,5*1000*9,81*8,20*4,10² =6,76 10⁵ N.

Calculer la hauteur à laquelle se trouve le centre de poussée sur les parois verticales, par rapport au fond de l'aquarium. OC = h/3 = 4,10/3 = 1,37 m.

Calculer la pression absolue p₃, entrée de la pompe à la profondeur Dz.

p₃ = rgDz+p_atm

p₃ =1000*9,81*21+ 1,00 10⁵ =3,06 10⁵ Pa.

Calculer la vitesse d'écoulement c₂ au point 2 ( sortie de la pompe) :

débit volumique (m³ s^-1) = section (m²) * vitesse (m/s)

q_v = pd²/4*c₂ ; c₂ = 4q_v /(pd²).

q_v = 60/3600 m³ s^-1; d = 0,052 m ; c₂ = 4*60/3600 / (3,14 *0,052²) =7,85 m/s.

En considérant la vitesse d'écoulement c₁ négligeable au point 1 ( à la surface libre de l'eau de l'aquarium),

calculer la pression absolue p₂ au point 2.

Entre les points 1 et 2 il n'y a pas de pompe ; le théorème de Bernoulli s'écrit :

g(z₂-z₁) +½(c₂²-c₁²) +(p₂-p₁)/r =0

z₂-z₁= -H = -30 m ; c₂ = 7,85 m/s ; p₁ = p_atm = 1,00 10⁵ Pa.

gH +½c₂² +(p₂-p₁)/r =0

p₂= p₁ - r (gH +½c₂²)

p₂= 10⁵ -1000 *(-9,81*30 +0,5*7,85²) =3,635 10⁵ =3,63 10⁵ Pa.

Calculer le débit massique de la pompe.

débit massique( kg s^-1) = débit volumique (m³ s^-1) * masse volumique (kg m^-3)

q_m = q_v r = 60/3600*1000=16,667 =16,7 kg s^-1.

Calculer la puissance P fournie par la pompe au fluide ( en considérant c₃=c₂)

g(z₂-z₃) +½(c₂²-c₃²) +(p₂-p₃)/r =P/q_m.

z₃=z₂ ; (p₃-p₂)/r =P/q_m.

P =q_m(p₂-p₃)/r .

P =16,667*(3,635 -3,06 ) 10⁵ / 1000 =958 W.