Aurélie 27/09/07
 

Mécanique des fluides : château d'eau BTS EEC 2007

(7 points)

Google

Un château d'eau alimente deux immeubles d'habitation repérés sur le schéma ci-dessous.

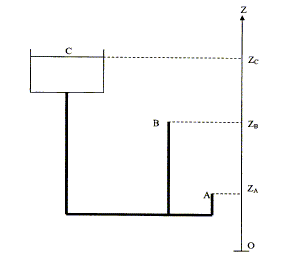
On modélise le système par deux arrivées d'eau munies chacunes d'un robinet. Les canalisations ont un diamètre d= 16 mm.

Le réservoir étant de grande taille, zC reste constant au cours du temps.

zB = 1090 m : altitude du robinet B de l'immeuble B

zA = 1050 m : altitude du robinet B de l'immeuble A

zC = 1100 m : altitude de la surface libre de l'eau contenue dans le château d'eau.

A la sortie du robinet ouvert, la pression de l'eau est égale à la pression atmosphérique P0 = 1,0 105 Pa.

masse volumique de l'eau r = 1000 kg m-3 ; g = 10 m/s2.

Enoncé le principe fondamental de la statique des fluides ?

La différence de pression PB-PA entre deux points A et B d'un fluide homogène, est proportionnelle à la différence de hauteur H=AB et à la masse volumique r du fluide.

PB-PA = r g H

 
Calculer la pression aux points A et B quand les robinets sont fermés. 

PA-PC= r g( zC-zA) ; PA=PC+r g( zC-zA) ; PA=P0+r g( zC-zA).

PA=1,0 105 + 1000*10 ( 100-1050) = 6,0 105 Pa.

PB=P0+r g( zC-zB).

PB=1,0 105 + 1000*10 ( 100-1090) = 2,0 105 Pa.

On ouvre le robinet A et on ferme le robinet B.

Calculer la valeur de la vitesse d'écoulement VA en A.

relation de Bernoulli : ½(VC2-VA2)+ g(zC-zA)+( PC-PA)/r = 0

On considère un point C de la surface libre de l'eau et un autre point A du jet d'eau à la sortie du robinet.

PC=PA = pression atmosphérique.

de plus VC = 0 , l'eau est immobile à la surface du château d'eau

d'où : -½VA2 + g(zC-zA) =0

VA2 = 2 g(zC-zA) ; VA = [2g(zC-zA)]½.

VA = [20*50]½= 32 m/s ( 31,62 )

Quel est le débit volumique QVA en L/s ?

QVA = VA pd2/4 avec d= 1,6 10-2 m

QVA = 31,62 * 3,14*(1,6 10-2 )2/4 = 6,4 10-3 m3/s = 6,4 L/s.

On ouvre le robinet B et on ferme le robinet A.

Calculer la valeur de la vitesse d'écoulement VB en B.

VB = [2g(zC-zB)]½.

VB = [20*10]½= 14 m/s ( 14,14 )

Quel est le débit volumique QVB en L/s ?

QVB = VB pd2/4 avec d= 1,6 10-2 m

QVB = 14,14 * 3,14*(1,6 10-2 )2/4 = 2,8 10-3 m3/s = 2,8 L/s.
On introduit une pompe avant le point B, de façon à ce que le débit volumique Q'VB = 6,35 L/s. Le robinet A est fermé.

Pu/QV =½r(V22-V21) +rg(Z2-Z1)+P2-P1.

Quelle est la puissance utile Pu de cette pompe ?

On considère un point C de la surface libre de l'eau et un autre point B du jet d'eau à la sortie du robinet.

P2=P1 = pression atmosphérique.

de plus VC = 0 , l'eau est immobile à la surface du château d'eau

d'où : Pu/QV =½rV2B +rg(ZB-ZC)

avec VB =Q'VB /(0,25pd2) =6,35 10-3 / (0,25*3,14*(1,6 10-2)2)=31,6 m/s ; ZB-ZC = - 10 m

Pu/QV = 500*31,62 - 1000*10*10 =4,0 105.

Pu = 4,0 105 *6,35 10-3 = 2,5 103 W.
retour -menu