|
Etude de la flottabilité d'un bateau ; moteur Diesel ; combustion du gasoil bts domotique 2007 |
||||
|
||||
|
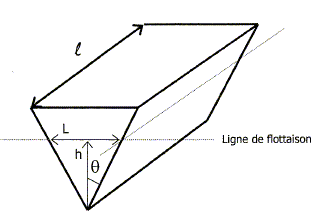
Pour simplifier les calculs, on assimile la coque du navire à un prisme schématisé ci-dessous :
On donne : masse du navire à vide 4600 tonnes ; charge maximum : 2000 tonnes. longueur du navire : l = 108 m ; masse volumique de l'eau de mer : reau = 1029,7 kg m-3 ; q= 54 ° Calculer la valeur du poids P du navire lorsqu'il est en charge maximum : P= mg avec m = 4600+2000 = 6600 t = 6,6 106 kg ; g = 9,8 N kg-1. P= 6,6 106 *9,8 = 6,468 107 N =6,5 107 N. Le volume immergé Vi du navire est donné par la relation : Vi = h2 l tan q. Montrer que la valeur de la force d'Archimède Fa exercée sur le navire peut s'exprimer en fonction de h par la relation : Fa= 1,5 106 h2. La poussée d'Archimède est égale au poids du volume dee fluide ( d'eau) déplacé. Fa = Vi reau g Fa = h2 l tan q reau g Fa =108 tan 54 * 1029,7 *9,8 Fa= 1,5 106 h2. A l'équilibre le
poids est égal à la poussée
d'Archimède. P=Fa ;
6,468 107 = 1,5 106
h2. 64,68 = 1,5 h2 ; h =
(64,68/1,5)½
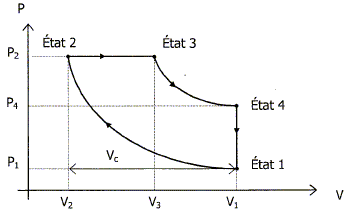
=6,6 m. Pour permettre la production d'énergie électrique sur le navire, deux salles sont équipées de groupes électrogènes. Chaque groupe est conposé d'un moteur Diesel, constitué de 8 cylindres en ligne, accouplé à un alternateur. L'étude porte sur un cylindre. Le diamètre de chaque cylindre est de 200 mm et la course du piston est de 279 mm. Le cycle théorique de ce moteur Diesel à 4 temps est constitué par les transformations suivantes : Transformation 1--> 2 : compression adiabatique réversible de l'air. Transformation 2 --> 3 : combustion isobare par injection de gazole. Transformation 3 --> 4 : détente adiabatique réversible des gaz. Transformation 4--> 1 : refroidissement isochore des gaz.
Les gaz décrivant ce cycle sont assimilables à de l'air et sont considérés comme parfaits. Lors d'essais en usine les valeurs suivantes ont été mesurées : état 1 : V1 = 9000 cm3 ; q1 = 21,2 °C ; P1 = 1,02 bar. état 2 : V2 ; q2 ; P2 ; état 3 : V3 ; q3 =1827 °C ; P3. état 4 : V4 ; q4=333 °C ; P4. Données : R = 8,31 SI ; g=1,4 ; capacité thermique molaire de l'air à pression constante Cp = 29 J mol-1 K-1. Expliquer les termes transformations isobare et isochore. isobare : la pression reste constante ; isochore : le volume reste constant. Montrer que le nombre initial de moles de gaz présentes à chaque cycle dans un cylindre est égal à n =0,375 mole. Loi des gaz parfaits : PV = nRT. avec à l'état 1 :V = 9000 cm3 = 9 10-3 m3 ;T = q1 +273 = 21,2+273 = 294,2 K ; P = 1,02 105 Pa ; R =8,31 SI. n = PV/ (RT) = 1,02 105*9 10-3 /(8,31*294,2) = 0,375 mol. La cylindréeVc représente le volume balayé par le piston. Montrer que Vc est égal à 8760 cm3. Vc = section du cylindre * course du piston ; Vc = pr2L avec r = 10 cm et L= 27,9 cm Vc = 3,14 * 102 * 27,2 = 8760 cm3.
En déduire la valeur du volume V2 : V2 = V-Vc = 9000-8760 = 240 cm3 = 2,4 10-4 m3. Calculer la pression P2 et la température T2. adiabatique réversible : P1 V1g = P2V2g. P2 = P1 (V1/V2)g = 1,02 (9000/240)1,4 =163 bar. loi des gaz parfaits : P2V2=nRT2 ; T2 =P2V2/(nR)= 1,63 105*2,4 10-4 / (0,375*8,31)=1255 K. Calculer la valeur de la quantité de chaleur Q23 échangée par les gaz au cours de la transformation isobare. Q23 = nCp(T3-T2) avec T3 =273+1827 = 2100 K Q23 = 0,375*29(2100-1255) =9,19 103 J. Calculer la valeur de la quantité de chaleur Q41 échangée par les gaz au cours de la transformation isochore. Q41 = nCv(T1-T4) avec Cv=Cp /g = 29/1,4 =20,7 J mol-1 K-1. Q41 = 0,375*20,7 (21,2-333) = -2,42 103 J. Quelles sont les quantités de chaleurs reçues par le gaz aux cours des transformations adiabatiques. Q12 =Q34 = 0. En appliquant le premier principe de la thermodynamique pour un cycle, calculer la valeur du travil W fourni au cours du cycle. La variation d'énergie interne du gaz est nulle sur le cycle : DU=W+Q=0. W= -Q = -(Q23+Q41 ) =(-9,19 +2,42) 103 = -6,8 103 J. Calculer le rendement théorique hth de ce moteur. hth = |W| / Q23 = 6,8 / 9,19 = 0,74 ( 74 %)
Etude de la combustion d'un moteur Diesel. La combustion du gasoil, de formule moléculaire C12H26 dans le dioxygène donne du dioxyde de carbone et de l'eau. L'air est composé, en moles, de 20% de dioxygène et de 80 % de diazote. Ecrire et équilibrer l'équation de combustion complète du gasoil. C12H26 +18,5 O2 = 12 CO2 + 13 H2O. Sachant que nair= 0,375 mol et qu'un cycle dure 0,12 s, déterminer le nombre de moles de gaz présentes dans l'air utile à la combustion en 1 s pour un moteur Diesel. Sur un cycle et pour un cylindre : nO2 = 0,2 nair = 0,2*0,375 =0,075 mol ; nN2 = 0,3 mol. En une seconde et sur un cylindre : nO2 =0,075*1/0,12 = 0,625 mol ; nN2 = 0,3 /0,12 =2,5 mol. En une seconde et sur 8 cylindres : nO2 =0,625*8= 5 mol ; nN2 = 2,5*8 =20 mol. En déduire la masse de gasoil correspondante. D'après les nombres stoechiométriques de l'équation ci-dessus : n(gasoil) = n(O2) /18,5 = 5/18,5 = 0,270 mol masse molaire du gasoil : 12*12+26 = 170 g/mol masse (g) = masse molaire (g/mol) * quantité de matière (mol) m = 170*0,27 = 45,94 g = 46 g. Calculer le volume de gasoil correspondant à cette masse. Donnée : densité du gasoil d = 0,85. volume (mL) = masse (g) / densité = 45,94 / 0,85 = 54 mL. La capacité de la cuve de gasoil est 1233 m3. Déterminer en jours l'autonomie du navire. 54 mL = 5,4 10-5 m3 consommé chaque seconde. 1233/ 5,4 10-5 =2,28 107 s = 264 jours. Puis diviser par le nombre de moteurs : 264/4 = 66 jours. |
||||
|
|
||||
|
|