isolation thermique; étude d'un siphon ; chimie organique d'après bts batiment 2006

Aurélie 20/12/6

Isolation thermique (7 points)

Un mur est constitué de l'intérieur vers l'extérieur par :

- Une cloison de placo-plâtre de résistance thermique pour 1 m², notée R_P.

- Une couche de laine de verre d'épaisseur e et de conductivité thermique l.

- Une paroi de béton de résistance thermique pour 1 m², notée R_B.

Les températures ambiantes interne et externe sont notées q_i et q _e. Les résistances thermiques superficielles intérieure et extérieure sont notées r_i et r_e.

Donner l'expression littérale du coefficient de transmission surfacique K en fonction des données. Calculer K
Donner l'expression littérale du flux thermique surfacique F à travers ce mur. Calculer F.
Donner les expressions littérales des températures superficielles intérieure q_si et extérieure q _se puis les calculer.

Données : R_P=0,8 m² KW^-1 ; R_B=0,30 m² KW^-1 ; r_i=0,06 m² KW^-1 ; r_e=0,12 m² KW^-1 ; e=10 cm ; l=0,04 W m^-1 K^-1 ; q_i = 20°C ; q_e= 40°C ;

corrigé

Résistance thermique R du mur et coefficient de transmission surfacique K :

R= r_e + R_B + e/l +R_P +r_i ; K= 1/R = 1/(r_e + R_B + e/l +R_P +r_i)

R= 0,12+0,3+0,1/0,04+0,8+0,06= 3,8 m² KW^-1 ; K= 1/3,8 = 0,26 W m^-2 K^-1.

flux thermique surfacique F à travers ce mur :

F = K(q_e-q_i) = 0,263 ( 40-20) = 5,3 W m^-2.

températures superficielles intérieure q_si et extérieure q _se :

F = 1/r_i (q_si-q_i) ; q_si-q_i = F r_i ; q_si = F r_i +q_i

q_si =5,3*0,06+20 = 20,3 °C.

F = 1/r_e (q_e-q_se) ; q_e-q_se = F r_e ; q_se = q_e-F r_e

q_se =40-5,3*0,12 = 39,4 °C.

Etude d'un siphon (7 points)

Un vase cylindrique de section S est fermé à sa partie supérieure par un couvercle muni d'un robinet R et laissant passer la branhe ED d'un siphon EDGF.

Ce vase renferme de l'eau dont le niveau MN est à une distance h du couvercle et à une hauteur H au dessus du robinet R' situé à l'extrémité du siphon.

Le siphon étant rempli d'eau et le robinet R' étant fermé, on ouvre un instant le robinet R et on le referme. La pression au dessus du liquide est alors égale à la pression atmosphérique notée P_atm.

La section du siphon est négligeable devant celle du vase.

On ouvre le robinet R' et on laisse l'eau s'écouler.

L'eau peut cesser de s'écouler avant que le récipient soit vide. Expliquer pourquoi à l'aide du théorème de Bernoulli.
Soit x l'abaissement du niveau MN à un instant donné et p la pression de l'air dans la partie supérieure du vase. On suppose la température constante pendant l'écoulement et on considère l'air comme un gaz parfait. Exprimer la pression p en fonction de x, h et P_atm.
Exprimer lorsque l'eau s'arrête de couler ( R' est toujours ouvert) la presion p en fonction de x, H, r et P_atm. Pour cela appliquer la relation fondamentale de l'hydrostatique au liquide contenu dans le siphon.

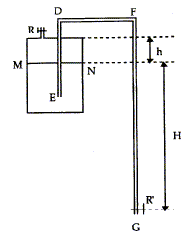
Données :S= 100 cm² ; h= 0,10 m ; H= 2,0 m ; g= 10 m/s² ; P_atm = 1,0 10⁵ Pa ; r= 1030 kg/m³.

corrigé

Equation de Bernoulli relative à une masse de 1 kg du fluide: ½(v₂²-v²₁) + g(z₂-z₁)+(P₂-P₁)/r=0.

état 2 ( point G) ; état 1 : surface du liquide dans le vase.

v₁=0 : la section S est très supérieure à la section du siphon ; v₂ =vitesse de l'eau en G

l'altitude de G est choisie comme origine z₂ =0 ; z₁ = H-x avec x, l'abaissement du niveau.

P₂ = pression atmosphérique ; P₁= p

d'où : ½v₂² - g(H-x)+(P₂-p)/r=0.

Si l'eau ne s'écoule plus alors v₂=0 ; g(H-x) =(P₂-p)/r.

H-x= (P₂-p)/(gr) ; x = H-(P₂-p)/(gr)

Dés que l'abaissement du n iveau atteint la valeur x = H-(p-P₂)/(gr) l'eau ne s'écoule plus.

Expression de la pression p en fonction de x, h et P_atm.

La température et la quantité de matière de l'air sont constants d'où PV= constante

volume initial de l'air au dessus de l'eau du vase : V₀= Sh

volume de l'air lorsque le niveau descend de x mètres :V= S(h+x)

par suite P_atmV₀= pV ; P_atmSh =p S(h+x) ; P_atmh =p (h+x) ;

p = P_atmh /(h+x) ; p = 10⁵*0,1/(0,1+x) = ; p = 10⁴/(0,1+x) (1)

Expression de la presion p en fonction de x, H, r et P_atm, lorsque l'eau s'arrête de couler ( R' est toujours ouvert) :

différence de hauteur entre le point G et la surface du liquide dont le niveau est descendu de x mètres : H-x

différence de pression P_atm-p = rg(H-x)

p = P_atm-rg(H-x) ; p = 10⁵-10300(2-x) ; p =10⁵- 1,03 10⁴(2-x) (2)

en combinant les relations (1) et (2) il vient :

10⁴/(0,1+x) = 10⁵- 1,03 10⁴(2-x) ; 1/(0,1+x) = 10-1,03(2-x); 10(0,1-x) -1,03(2-x)(0,1-x)= 1

x² + 7,81 x -0,2 = 0 ; solution x = 0,0255 m ; x= 2,55 cm.

chimie organique (6 points)

Choisir la bonne réponse :

Question réponse A réponse B réponse C réponse D

Quel est l'hydrocarbure de masse molaire 28g/mol ?
C : 12 g/mol ; H : 1 g/mol c'est un alcane : l'éthane c'est un alcyne : l'éthylène c'est un alcène : l'éthène C₂H₄ c'est un alcène : l'acéthylène

Quel est le nom du composé ? l'éthylpropane le 2-méthylbutane le pentane le 1,1-diméthylpropane

Une macromolécule d'indice de polymérisation n= 2500 a une masse molaire M= 105 kg/mol. Quelle est la masse molaire du monomère ? 105 000 / 2500 =
42 g/mol
0,042 g/mol 2,625 10⁵ kg/mol 24 g/mol

Quelle est la formule du PVC ?
réponse B

Le pH d'un composé organique de concentration c=0,5 mol/L vaut 2,6. Ce composé est : un acide fort une base faible une base forte un acide faible
pH>-log c

Les équations-bilan ci-dessous correspondent respectivement aux types de réactions :
addition
combustion

polymérisation

substitution
combustion
addition

polymérisation

substitution
polymérisation
substitution

combustion

addition
combustion
addition

substitution

polymérisation

retour -menu