|
transformations spontanées ou forcées ? solution de bromure de cuivre (II) bac Amérique du sud 2007 |
||||||
|
||||||
|
Données : masse molaire atomique du cuivre : M(Cu) = 63,5 g.mol-1 ; 1 faraday = 96500 C.mol-1 ; charge électrique élémentaire : e = 1,602 10-19 C ; constante d'Avogadro : NA = 6,02 1023 mol-1. On considérera que 8,3 10 -26 voisin de zéro.. Réaction entre le cuivre métal et le dibrome en solution aqueuse. Dans un becher, on verse 100 mL de solution aqueuse jaune de dibrome (Br2(aq)) telle que [Br2] = 1,0 10-2 mol/L et on y ajoute, sans variation de volume, de la poudre de cuivre en excès. On place sous agitation. Après filtration, on observe la disparition de la coloration jaune et on obtient un filtrat de couleur bleue. L'équation de l'équation associée à la transformation est : Cu(s) + Br2(aq) = Cu2+(aq) + 2 Br - (aq). La constante d'équilibre associée à cette réaction est K1 = 1,2 1025. Donner l'expression du quotient de réaction initial. Calculer sa valeur. Qr, i = [Cu2+]i [Br-]i2 /[ Br2]i Or [Cu2+]i = [Br-]i =0 donc Qr, i =0. Dans quel sens le système va-t-il évoluer ? Justifier la réponse. Qr, i <K, le système évolue dans le sens direct d'après le critère d'évolution spontané. La transformation est-elle forcée ou spontanée ? La transformation est spontanée, elle ne nécessite aucun apport d'énergie sous forme électrique.
Dans un becher, on verse 100 mL d'une solution
aqueuse de bromure de cuivre (II). Les concentrations des ions en solution sont :
[Cu2+(aq)] = 0,50
mol.L-1 et [Br -(aq)]
=1,0 mol.L-1 . Au sein de cette solution, on pourrait envisager une réaction entre les ions Cu2+(aq) et Br - (aq). L'équation de cette réaction serait : Cu2+(aq) + 2 Br - (aq) = Cu(s) + Br2(aq) La constante d'équilibre associée à cette réaction est K2= 8,3 10-26. Calculer la valeur du quotient de réaction initial. Qr, i = [ Br2]i / ([Cu2+]i [Br-]i2 ) Or [ Br2]i =0 donc Qr, i =0. Quelle sera la valeur de ce quotient à l'équilibre ? A l'équilibre la valeur du quotient de réaction est égal à la constante d'équilibre. Qr, éq =K2= 8,3 10-26 proche de zéro ( d'après l'énoncé). Justifier l'affirmation "la solution aqueuse de bromure de cuivre (II) est stable". Qr, i= K2 en conséquence la solution aqueuse de bromure de cuivre (II) est dans un état d'équilibre stable.
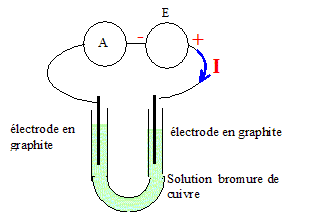
Pour conduire cette électrolyse, on réalise le montage représenté ci-dessous.
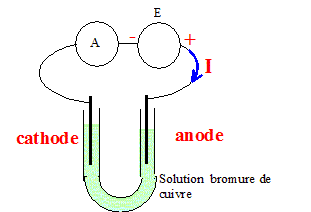
Sur le schéma du montage représenté est indiqué le sens conventionnel du courant électrique imposé par le générateur. Identifier l'anode et la cathode. L'anode est reliée à la borne positive du générateur.
Écrire la demi équation de la réaction qui a lieu à l'anode. Oxydation des ions bromures à l'anode : 2Br- (aq) = Br2(aq) + 2e-. Écrire la demi équation de la réaction qui a lieu à la cathode. Réduction des ions cuivre (II) : Cu2+(aq) + 2e- = Cu(s). Écrire l'équation de la réaction d'électrolyse. Cu2+(aq) +2Br - (aq) = Br2(aq) +Cu(s). La transformation associée à la réaction d'électrolyse est-elle spontanée ou forcée ? La transformation nécessite un apport d'énergie sous forme électrique. Une électrolyse est une transformation forcée.
L'électrolyse est effectuée pendant 1 heure avec un intensité constante I = 1,00 A. Calculer : La quantité d'électricité Q qui a traversé la solution de bromure de cuivre (II). Q= I t avec Q ( coulomb) ; I : ampère et t en seconde. Q= 1,00*3600 = 3,60 103 C. La quantité de matière (en mol) d'électrons qui a été mise en jeu. Q= n e avec n ( mol) et e la charge élémentaire. n = 3600/96500 =3,73 10-2 mol. La quantité de matière (en mol) de cuivre qui s'est formée. On pourra s'aider d'un tableau d'évolution du système. Cu2+(aq) + 2e- = Cu(s). d'après les nombres stoechiométriques n(Cu) = ½n(e-) = 1,8653 10-2 mol = 1,87 10-2 mol. La masse de cuivre obtenue. masse (g) = masse molaire (g/mol) * quantité de matière (mol) m = 63,5*1,8653 10-2 = 1,18 g.
|
||||||
|
|
||||||
|
|