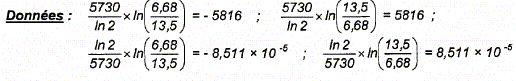Aurélie 12/06/07
 

Radioactivité, datation au carbone 14 bac S 2007 La Réunion 

Google

Sans calculatrice ; 4 pts ; d'autres corrigés labolycee.org ; intellego.fr ; montblancsciences.free.fr.

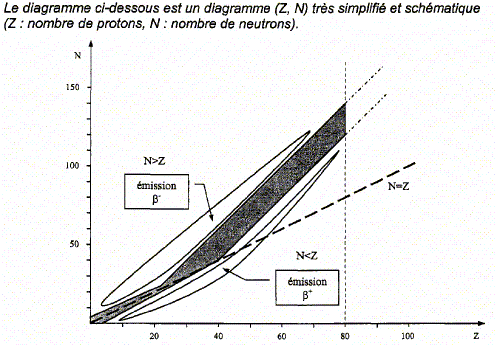
La radioactivité naturelle fut découverte en 1896 par H. Besquerel. Le signe le plus perceptible de la radioactivité est l'existence d'un rayonnement émis par les atomes de certains nucléides et dont l'origine se situe au niveau de leur noyau qui est instable. On observe ainsi, par exemple, les rayonnements ( on parle de radioactivité) b ( béta+ ou béta-), qui s'accompagnent souvent d'émission g ( gamma), radiation électromagnétique de même nature que la lumière, provenant du retour à l'état fondamental d'un noyau fils suite à la transmutation d'un noyau père radioactif.

Equation de la désintégration nucléaire, diagramme (Z, N) :

Parmi les trois types de radioactivité étudiés en classe, citer celle qui n'a pas été évoquée dans le texte plus haut. Donner la composition de la particule émise lors de cette radioactivité.

Que représente la zone grisée dans ce diagramme ?

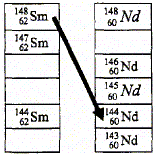
Soit la réaction nucléaire de transmutation indiquée par la flèche ci-contre. Sachant qu'une seule particule est émise en plus du noyau fils, écrire cette réaction de désintégration nucléaire et indiquer les deux lois de conservation ( lois de Soddy) qui régissent toute réaction nucléaire.

Quel type de radioactivité concerne la réaction précédente ?

Parmi les trois types de radioactivité étudiés en classe, la radioactivité de type a n'a pas été évoquée dans le texte plus haut.

La particule émise lors de cette radioactivité est un noyau d'helium 42He ( 2 protons et 4-2 = 2 neutrons).

La zone grisée du diagramme représente la "vallée de la stabilité ", ensemble des noyaux stables.

Soit la réaction nucléaire de transmutation indiquée par la flèche ci-dessus :

14862 Sm---> 14460 Nd + AZX

Conservation du nombre de nucléons : 148=144+A soit A=4.

Conservation de la charge : 62 = 60 + Z soit Z=2 ; donc élément hélium

La particule émise est un noyau d'hélium 42He : la radioactivité de type a.
De toutes les méthodes radio-chronologiques ( basées sur la loi statistique de Curie-Rutherford-Soddy ou loi de décroissance radioactive), celle de la datation au carbone 14 est la plus connue. Dans la haute atmosphère, soumis au rayonnement cosmique galactique constitué de protons, des neutrons secondaires interagissent avec les noyaux d'azote 14. Cette réaction forme un isotope AZX du carbone : le fameux carbone 14. Immédiatement formé le carbone 14 s'oxyde en se combinant avec l'oxygène pour former du dioxyde de carbone qui se mélange avec le reste de l'atmosphère. Or le carbone 14 est radioactif. La teneur en carbone 14 est constante dans le monde ( dans l'atmosphère comme dans chaque organisme vivant ). Cela est du à un équilibre entre la désintégration et la production de carbone 14. Chaque gramme de carbone contient des atomes de carbone 14. On enregistre en moyenne 13,5 désintégrations par minute et par gramme de carbone. Lorsqu'un arbre, par exemple, est abattu, le bois cesse de vivre, le processus de photosynthèse s'arrête et il n'y a plus d'absorption de dioxyde de carbone. Le carbone 14 est alors libre de se désintégrer sans compensation. On peut donc dater l'âge de la mort de l'organisme ( au moment où cesse tout échange de CO2 avec l'atmosphère).
Données : 6C ; 7N.

Formation du carbone 14 dans la haute atmosphère :
L'azote 14 et le carbone 14 sont-ils isotopes ? Justifier.

Dans la haute atmosphère la réaction qui a lieu entre le neutron et le noyau d'azote 14 s'écrit : 147N + 10n---> AZX + 11p.

Vérifier, en justifiant avec les lois de conservation, que AZX est bien du carbone 14.

Deux noyaux isotopes ne se différentient que par leurs nombres de neutrons : ils ont le même n° atomique Z.

L'azote 14 147N et le carbone 14 146C ne sont donc pas isotopes.

147N + 10n---> AZX + 11p

Conservation de la charge : 7 = 1+Z d'où Z= 6, élément carbone.

Conservation du nombre de nucléons : 14+1 = A+1 d'où A = 14.

Décroissance du carbone14 :

L'étude de l'évolution de la population moyenne d'un ensemble de noyaux radioactifs permet d'écrire : DN= - l N Dt où N est le nombre de noyaux à la date t et DN est la variation du nombre de noyaux pendant la durée Dt. Cette relation conduit à la loi de décroissance radioactive N(t) = N0 exp (-lt), dans laquelle N0 est le nombre de noyaux à la date t=0.

  1. Comment se nomme l ?
  2. La demi-vie du carbone 14 est t½ = 5730 ans. Donner la définition de la demi-vie ou période du carbone 14.
    - En utilisant la loi de décroissance radioactive montrer que     l est lié à la demi vie t½ par la relation : l = ln2 /t½.
    - Par une analyse dimensionnelle, déterminer l'unité de     l.
  3. On rappelle que l'activité A d'un échantillon radioactif est le nombre de désintégrations par seconde. Montrer que l'activité A à l'instant t et le nombre N de noyaux présents dans l'échantillon à la date t sont liés par la relation : A = l N.
  4. Calculer en faisant apparaître l'application numérique, le nombre N d'atomes de carbone 14 dans 1 g de carbone tel que A= 13,5 désintégrations par minute et par gramme de carbone.
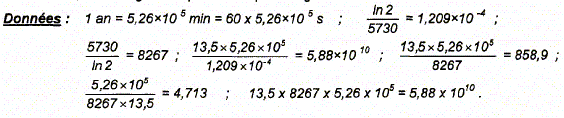
l est la constante radioactive.

Définition de la demi-vie ou période du carbone 14 :

Durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.
N(t½) = N0 exp (-lt½) ; N(t½) =½ N0

d'où : 0,5 N0 = N0 exp (-lt½) ; 0,5 = exp (-lt½)

ln 0,5 = -lt½ ; -ln 2 = - lt½ ;

l = ln2 /t½.
Unité de l :

ln 2 est sans dimension ; t½ a la dimension d'un temps donc [ln2 /t½] = T-1.

La constante radioactive est l'inverse d'un temps.

Montrons que l'activité A à l'instant t et le nombre N de noyaux présents dans l'échantillon à la date t sont liés par la relation : A = l N.

A = - dN/dt avec N = N0 exp (-lt)

dN/dt = -l N0 exp (-lt) = - l N

d'où A = l N.

Calcul du nombre N d'atomes de carbone 14 dans 1 g de carbone tel que A= 13,5 désintégrations par minute et par gramme de carbone :

N = A/l avec A = 13,5 / 60 Bq.

l = ln2 /t½ ; 1/l = t½/ ln2 avec t½ = 5730 ans = 60*5,26 105 s.

N= 13,5 / 60 * 5730*60*5,26 105 / ln 2 = 5730 / ln 2 *13,5*5,26 105

N=8267*13,5*5,26 105 = 5,88 1010.

 

 

Datation au carbone 14 :

La loi de décroissance radioactive peut également s'écrire en fonction de l'activité , A(t) =A0 exp (-lt), dans laquelle A0 est l'activité à la date t=0 et A l'activité mesurée à l'instant t.

Le prélèvement d'une poutre en bois dans une tombe au Sahara fournit une activité au moment de la mesure telle que A= 6,68 désintégrations par minute et par gramme de carbone alors que A0 = 13,5 désintégrations par minute et par gramme de carbone.

Démontrer que l'expression qui permet de donner l'âge de la mort d'un organisme s'écrit : t = t½ / ln 2 * ln(A0/A) avec t½ = 5730 ans.

Calculer en faisant apparaître l'application numérique, l'âge t de la tombe de ce vizir de la première dynastie des pharaons.

A(t) =A0 exp (-lt) avec l = ln2 / t½.

A(t) /A0 = exp (-lt) ; ln [A(t) /A0 ] = -lt ; ln [A0/A(t) ] =lt ;

ln [A0/A(t) ] = t ln2 / t½ ; t = t½ / ln 2 * ln(A0/A)

t =5730 / ln2 * ln(13,5 / 6,68) = 5816 ans.
 
retour -menu