|
bac S Polynésie 2007 : stimulateur cardiaque, décharge d'un condensateur, pile au lithium. |
|||||||||||
|
|||||||||||
|
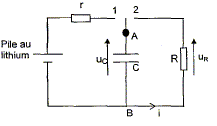
Un stimulateur cardiaque est un dispositif hautement perfectionné et très miniaturisé, relié au cœur humain par des électrodes appelées sondes. Le simulateur est actionné grâce à une pile intégrée, généralement au lithium ; il génère de petites impulsions électriques de basse tension qui forcent le cœur à battra à un rythme régulier et suffisamment rapide. Il comporte donc deux parties : le boîtier, source des impulsions électriques, et les sondes, qui conduisent le courant. Le générateur d'impulsions du simulateur cardiaque peut être modélisée par le circuit représenté ci-dessous : La valeur de r est très faible de telle sorte que le condensateur se décharge très rapidement lorsque l'interrupteur ( en réalité un dispositif électronique) est en position 1. Lorsque la charge est terminée, l'interrupteur bascule en position 2. Le condensateur se décharge lentement dans la résistance R, de valeur élevée. Quand la tension aux bornes de R atteint une valeur donnée ( e-1 fois sa valeur initiale avec ln e = 1), le boîtier envoie au cœur une impulsion électrique par l'intermédiaire des sondes. Un interrupteur bascule simultanément en position 1 et la recharge du condensateur se fait quasiment instantanément à travers r. Le processus recommence. D'après physique, TS, Ed
Bréal.
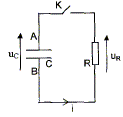
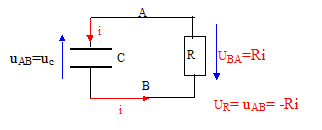
Pour déterminer la valeur de la résistance R, on insère le condensateur préalablement chargé sous la tension E dans le circuit schématisé ci-dessous C= 0,40 mF.
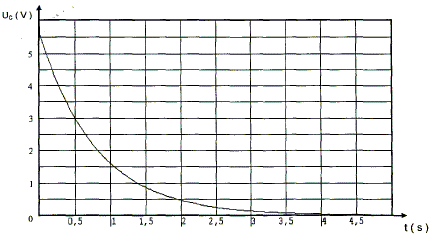
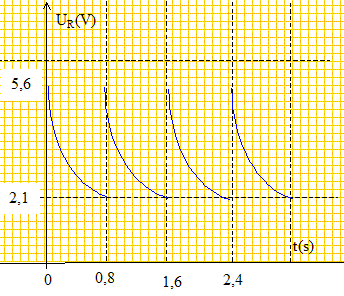
On enregistre alors l'évolution de la tension uc aux bornes du condensateur. La courbe obtenue est donnée ci-dessous.
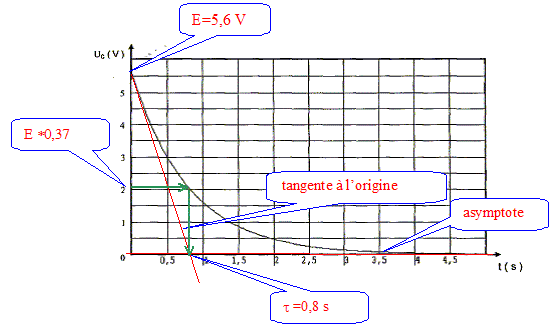
Déterminer graphiquement la valeur de la tension E. Déterminer graphiquement la
valeur de la constante de temps t
correspondant à la décharge du condensateur en
justifiant.
En respectant les notations du schéma ci-dessus, donner : La relation liant l'intensité i et la charge q de l'une des armatures du condensateur, que l'on précisera. La relation liant uR et i. En déduire que la tension aux bornes du condensateur vérifie l'équation différentielle 1/(RC) uc(t) + duc/dt = 0 Montrer que cette équation différentielle admet une solution de la forme uc(t) = A exp( -t/t) Donner les expressions de A et t en fonction de E, C et R. En utilisant la valeur de t, calculer la valeur de R. Les impulsions : On admet pour la suite que, tant que le condensateur se décharge, l'évolution de uR en fonction du temps est donnée par : uR(t) = 5,6 exp( -t/0,80) On rappelle qu'une impulsion électrique est envoyée au cœur lorsque la tension aux bornes de R atteint e-1 fois sa valeur initiale. Calculer la valeur de uR qui déclenche l'envoi d'une impulsion vers le cœur. A quelle date après le début de la décharge du condensateur, cette valeur est-elle atteinte ? Que se passe t-il après cette date ? Représenter l'allure de l'évolution de uR au cours du temps lors de la génération d'impulsions. Préciser les valeurs remarquables Déterminer la
fréquence des impulsions de tension ainsi
générées. On exprimera le
résultat en Hertz puis en impulsions par minute.
Vérifier que le résultat est bien compatible
avec une fréquence cardiaque normale.
i = dq/dt. Relation liant uR et i : On a refait le schéma en convention récepteur : ( la flèche qui représente i et celle qui repésente uR sont de sens contraire).
Additivité des tensions : uAB+uBA=0 ; uc+Ri = 0 (1) Or i = dq/dt et q= Cuc d'où i = Cduc/dt. (1) s'écrit : uc+RCduc/dt =0 équation différentielle 1/(RC) uc(t) + duc/dt = 0 (2) Montrons que cette équation différentielle admet une solution de la forme uc(t) = A exp( -t/t) : Calculer la dérivée duc/dt = -A/ t exp( -t/t) ; repport dans (2) 1/(RC) A exp( -t/t) -A/ t exp( -t/t) =0 Cette égalité est vérifiée quel que soit t si : t = RC. De plus à la date t=0, le condensateur est chargé ; la tension à ses bornes vaut E : d'où A= E. Calcul de R : C= 0,40 mF = 4 10-7 F ; t = 0,80 s R= t/C = 0,80 / 4 10-7 = 2 106 W. Les impulsions : uR(t) = 5,6 exp( -t/0,80) Une impulsion électrique est envoyée au cœur lorsque la tension aux bornes de R atteint e-1 fois sa valeur initiale. Valeur de uR qui déclenche l'envoi d'une impulsion vers le cœur. 5,6 e-1 = 5,6 * 0,368 = 2,1 V. A quelle date après le début de la décharge du condensateur, cette valeur est-elle atteinte ? 5,6 e-1 = 5,6 exp( -t/0,80) ; e-1 =exp( -t/0,80) ; -1 = -t/0,80 ; t = 0,80 s. Après cette date : "Un interrupteur bascule simultanément en position 1 et la recharge du condensateur se fait quasiment instantanément à travers r. " Allure de l'évolution de uR au cours du temps lors de la génération d'impulsions.
La période T, durée séparant deux impulsions successives vaut T= 0,8 s ; la fréquence des impulsions de tension ainsi générées vaut : f = 1/T = 1/0,8 = 1,25 Hz ( 1,3 Hz) ou 1,25*60 = 75 impulsions par minute. Cette valeur correspond à la fréquence cardiaque normale d'une personne au repos.
Etude d'une pile au lithium Les différents types de pile au lithium ont toutes en commun une électrode au lithium et un électrolyte constitué d'un solvant organique contenant entre autres des ions lithium Li+. L'équation de la réaction qui se produit à cette électrode est : Li = Li+ + e-. Masse molaire du lithium 6,9 g/mol ; valeur du faraday : 9,65 104 C. Fonctionnement de la pile Pour chacune des affirmations suivantes répondre par vrai ou faux. L'électrode de lithium est le pôle négatif de la pile. Lors de son fonctionnement, la pile constitue un système chimique en équilibre. Lors de son fonctionnement, le quotient Qr de la réaction qui se produit est inférieur à la constante d'équilibre K correspondante. La pile est usée quand tous les ions Li+ sont consommés. Quantité d'électricité fournie par la pile Montrer par analyse dimensionnelle qu'une quantité d'électricité peut s'exprimer en Ah et justifier l'égalité 1 Ah = 3600 C Calculer en coulomb, puis en Ah, la quantité d'électricité que pourrait fournir la pile contenant 1,0 g de lithium. Intérêt du lithium Le tableau suivant rassemble les capacités massiques de stockage de plusieurs éléments entrant dans la composition de différents types de piles. Cette capacité massique est la quantité d'électricité que peut débiter la pile par kg d'élément constituant. Elle peut s'exprimer en A h kg-1.
Pourquoi utilise t-on des piles au lithium pour alimenter les stimulateurs cardiaques ?
L'électrode de lithium est le pôle négatif de la pile. Vrai. Li = Li+ + e-. oxydation du lithium qui libère des électrons. Lors de son fonctionnement, la pile constitue un système chimique en équilibre. Faux. La pile est le siège de réactions d'oxydoréduction. Lors de son fonctionnement, le quotient Qr de la réaction qui se produit est inférieur à la constante d'équilibre K correspondante. Vrai. Evolution naturelle spontanée vers un état d'équilibre. La pile est usée quand tous les ions Li+ sont consommés. Faux. La pile est usée lorsque le lithium métallique, le réducteur, est consommé. Quantité d'électricité fournie par la pile Une quantité d'électricité ( exprimée en coulomb (C)) est une intensité ( ampère (A)) multipliée par un temps ( seconde) Une quantité d'électricité ( exprimée en ampère heure (Ah)) est une intensité ( ampère (A)) multipliée par un temps ( heure) 1 h = 3600 s donc 1 Ah = 3600 C. Quantité d'électricité que pourrait fournir la pile contenant 1,0 g de lithium. Li = Li+ + e- donne n( Li) = n(e-). De plus n( Li) (mol) = masse (g) / masse molaire (g/mol) = 1,0 / 6,9 = 0,145 mol. Q= n(e-) * 9,65 104 = 0,145 * 9,65 104 =1,4 104 C soit 1,4 104 / 3600 = 3,9 Ah. Intérêt du lithium Pour une même intensité de courant électrique débité, la durée de fonctionnement de la pile augmente en fonction de sa capacité massique. Les piles au lithium utilisées pour alimenter les stimulateurs cardiaques ont une grande capacité massique : elles peuvent fonctionner longtemps sans intervention chirurgicales pour les renouveler. De plus, sous un faible volume, elles stockent une quantité d'électricité importante : le stimulateur peut ainsi être miniaturisé. |
|||||||||||
|
|
|||||||||||
|
|