|
Pendule : aspect énergétique ; vitesse ; accélération bac S 2002 Amérique du sud
|
|||
|
|||
|
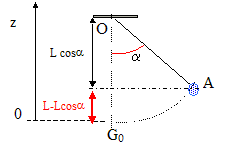
Ce pendule est constitué du mobile à coussin d'air de masse m=0,236 kg, adapté à la table, suspendu à l'extrémité d'un fil inextensible et de masse négligeable devant celle du mobile. L'autre extrémité du fil est accrochée en un point fixe O. Ce pendule est assimilé à un pendule simple de longueur L=OG= OG0=0,41 m.
On enregistre les positions du centre d'inertie G du mobile toutes les 30 ms. On note t= 30 ms.
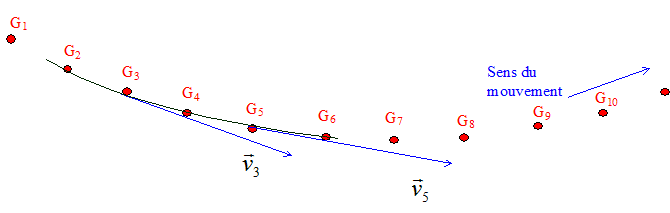
G2G3=1,6 cm ; G3G4=1,7 cm ; G4G5=1,8 cm ; G5G6= 1,8 cm. Valeurs v3 et v5 des vecteurs vitesses aux points G3 et G5 : v3 = (G2G3+G3G4)/ (2t) = (16+17)/ (2*30) = 33/60 = 0,55 m/s. v5 = (G4G5+G5G6)/ (2t)=(18+18)/ (2*30) = 36 /60 = 0,60 m/s. Représentation de ces vecteurs ( 1 cm <--> 0,1 m/s): Les vecteurs vitesses sont portés par la tangente la trajectoire au point considéré ; le sens est celui du mouvement.
Valeur a4 du vecteur accélération du centre d'inertie au point G4 :
Mesurer Dv4 : 1,1 cm ; tenir compte de l'échelle : Dv4 = 0,11 m/s a4 = Dv4 /(2t) =0,11/(60 10-3) = 1,8 m s-2.
Expression de l'énergie cinétique du pendule simple : Ec = ½mv2 ; m: masse (kg) ; v: vitesse (m/s) ; Ec ( J). Expression de l'énergie potentielle de pesanteur du pendule simple : La position d'équilibre G0 est choisie comme origine.
Epp = mgz = m g L(1-cos a) avec L =OAen mètre Expression de l'énergie mécanique du pendule : Em = Epp + Ec = m g L(1-cos a) + ½mv2 .
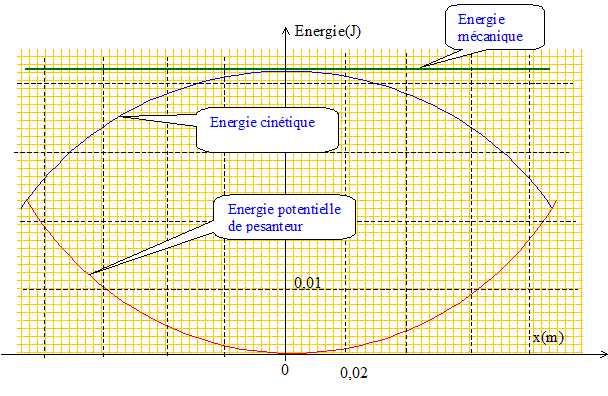
Valeur de la vitesse maximale du pendule : Le graphe indique que l'énergie mécanique est égale à 0,042 J Au passage à la position d'équilibre G0, l'énergie mécanique est sous forme cinétique : ( vitesse maximale) 0,042 = ½mv2max ; vmax = (2*0,042/m)½ = (0,084/0,236)½ ; vmax = 0,60 m/s. Hauteur maximale atteinte par le pendule : L'énergie mécanique est sous forme potentielle de pesanteur. 0,042 = mg zmax ; zmax = 0,042/(mg) = 0,042/ (0,236*9,8) ; zmax = 0,018 m. Abscisse angulaire maximale a du pendule : 0,018 = L(1-cos amax) 1-cos amax= 0,018/L ; cos amax=1-0,018/L cos amax=1-0,018/ 0,41 =0,956 ; amax= 17 °.
Faire l'analyse dimensionnelle des quatre formules suivantes. En déduire la période T0. T0 = 2p mg/L ; T0 = 2p (g/L )½ ; T0 = 2p (L/g ) ; T0 = 2p (L/g )½. 2p : sans dimension ; L est une longueur ; g est une accélération soit une longueur / temps2. [L/g ] = T2 ; [ (L/g )½] = T. T0 = 2p (L/g )½. Dans la réalité, au cours du temps, du fait des frottements, les oscillations sont légèrement amorties. L'énergie mécanique diminue : une partie de celle-ci est dissipée sous forme de chaleur. |
|||
|
|
|||
|
|