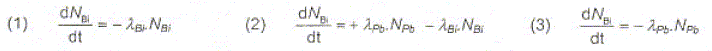|
radioactivité tellurique : compteur Geiger Müller ; le radon 222 ; le plomb 214 bac Nlle Calédonie 2007 |
||||||
|
||||||
|
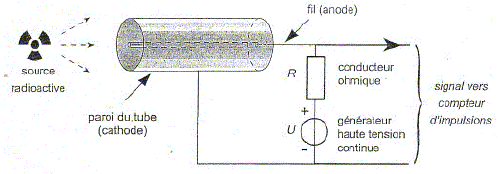
Le compteur Geiger Müller. Le tube Geiger Mülle, mis au point en 1928, est aujourd'hui encore un appareil indispensable pour la mise en évidence d'un rayonnement radioactif. Il est constitué d'un tube cylindrique rempli d'argon sous faible pression, dans lequel un fil conducteur est tendu le long de son axe. Une tension U de quelques centaines de volts est appliquée en permanence entre la paroi cylindrique du tube, qui sert de cathode, et le fil, qui joue le rôle d'anode via un conducteur ohmique de résistance R.
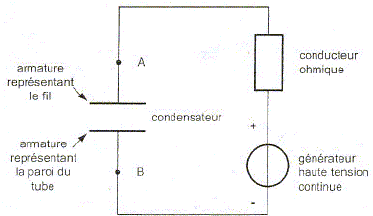
Circuit RC. Le tube constitué de la paroi extérieure et du fil central, rempli d'argon, soumis à la tension U=500 V forme un condensateur de forme cylindrique, de faible capacité C= 1,0 10-11 F. L'association du tube et du conducteur ohmique constitue un circuit RC série schématisé ci-dessous. Par souci de simplification le tube est modélisé par un condensateur plan.
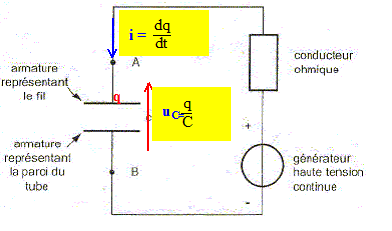
Représenter la flèche tension uC aux bornes du condensateur en respectant la convention récepteur, q désignant la charge du condensateur.
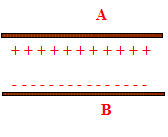
Rappeler l'expression de l'intensité du courant i en fonction de la charge q. i = dq/dt. En déduire la valeur de l'intensité I du courant, une fois que le condensateur a atteint sa charge maximale Q. Justifier. La charge maximale Q est constante. En conséquence dQ/dt =0 et donc I=dQ/dt =0. Calculer la valeur de la charge Q dans ces conditions. La tension aux bornes du condensateur est égale à la tension Uaux bornes du générateur. ( la tension aux bornes du résistor étant nulle I=0) Q= CU. Q= 1,0 10-11 *500 = 5,0 10-9 C. Indiquer par des charges + et - la répartition des charges sur les armatures du condensateur chargé. Les électrons se déplaçant en sens contraire de l'intensité, vont s'accumuler sur l'armature B du condensateur.
Impulsion de décharge. Dans le tube, une particule émise par désintégration radioactive ionise les atomes d'argon sur sa trajectoire. Chaque atome ionisé donne naissance à deux particules : un ion argon et un électron. Les ions positifs dérivent vers la paroi du tube. Les électrons sont accélérés vers le fil et provoquent par collisions successives d'autres ionisations. Il en résultee alors une brève diminution de tension entre les électrodes du tube, appelée "impulsion de décharge". Un compteur enregistre le nombre d'impulsions relevées pendant une durée du comptage donnée. La durée moyenne d'une impulsion de décharge consécutive à la détection d'une particule est Dt=0,10 ms. Pour un bon fonctionnement du compteur, la valeur de la constante de temps du circuit RC vérifie la condition t = 2Dt. Calculer la valeur de la résistance R. t =RC= 2Dt. R = 2Dt / C = 2*1,0 10-4 / 1,0 10-11 = 2,0 107 W. Montrer que la charge de l'anode diminue pendant la traversée de la particule. "Les électrons sont accélérés vers le fil et provoquent par collisions successives d'autres ionisations". Or le fil, l'anode, porte une charge positive. En conséquence la charge du fil va diminuer. Expliquer l'affirmation du texte :"Il en résultee alors une brève diminution de tension entre les électrodes du tube" La charge q de l'anode diminue ; or uC= q/C ; en conséquence la tension aux bornes du condensateur diminue. Pour modéliser le phénomène, on considère que le passage de la particule dans le tube engendre N électrons et N ions argon. Montrer que la diminution de tension aux bornes du condensateur est DuC= -Ne/C avec e : charge élémentaire. La charge q de l'anode diminue de la quantité Dq = -Ne. or uC= q/C ; en conséquence : DuC= Dq /C = - Ne/C.
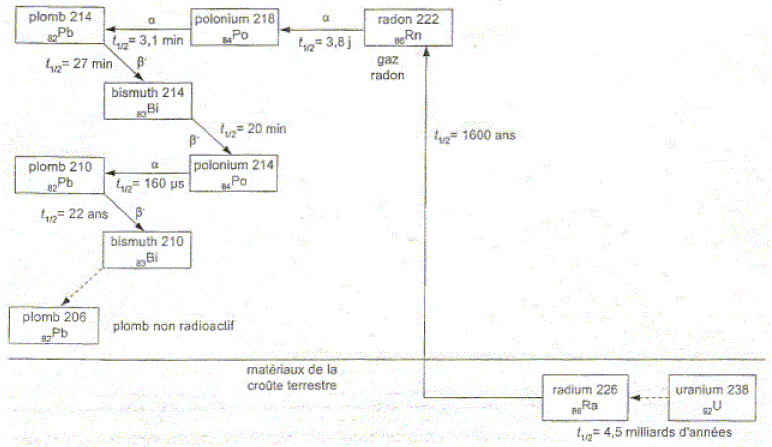
Les roches de l'écorce terrestre renferment de l'uranium 238 radioactif. Après plusieurs désintégrations successives, il se forme du radon 222, principal responsable de la radioactivité dite tellurique. ce radon s'échappe, à l'état gazeux, des roches et s'infiltre dans les fissures des fondations des bâtiments et s'accumule dans les locaux non ventilés. Famille de l'uranium 238. Les descendants du radon 222 appartiennent à la famille décrite ci-dessous. Chaque flèche pleine désigne une désintégration, les flèches en pointillés représentent une succession de désintégrations.
Indiquer la composition du noyau de radon 222. 22286Rn 222 nucléons dont 86 protons et en conséquence 222-86 =136 neutrons. Que peut-on dire des noyaux représentés sur une même verticale. Justifier. Ces noyaux appartiennent au même élément chimique ( même numéro atomique) Ils possèdent des nombres de neutrons différents : ce sont des isotopes. Ecrire l'équation de désintégration du radon 222 et celle du plomb 214. 22286Rn --> 21884Po +42He 21482Pb --> 21483Bi +0-1e Quel est le nom et la signification de la grandeur t½ reportée sur la flèche de désintégration de chaque noyau. t½ est la demi vie ( ou période) radioactive : c'est la durée au bout de laquelle la moitié des noyaux présents initialement se sont désintégrés. C'est la durée au bout de laquelle l'activité initiale a diminué de moitié. Donner sa valeur pour le polonium 218. 3,1 min.
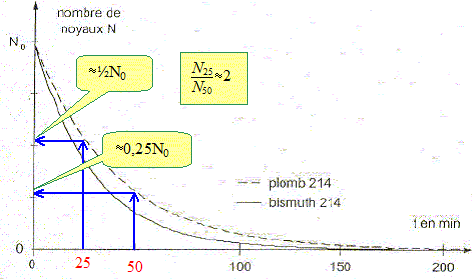
Un aspirateur muni d'un filtre permet de récupérer des poussières de l'air ambiant. On étudie alors l'évolution temporelle de la radioactivité de ces poussières à l'aide d'un compteur Geiger Müller. L'activité mesurée est celle des noyaux descendants du radon 222, fixés sur les microparticules piégées dans le filtre. L'objectif de cette partie est de montrer que deux noyaux descendants de la famille de l'uranium 238 sont principalement détectés par le compteur. On transporte ce filtre et on le dépose dans le détecteur une dizaine de minutes après l'aspiration. Par combien est approximativement divisé le nombre de noyaux de polonium 218 entre la fin de l'aspiration et le début des mesures dans le détecteur : par 2, 4, 5 ou 8 ? Justifier. Une dizaine de minutes correspond à peu près à 3 fois la demi-vie du polonium 218. A chaque demi-vie, l'activité est divisée par 2 ; au bout de trois demi-vies l'activité est divisée par 23 = 8. On admet que l'activité du polonium 218 dans le local aspiré, proportionnelle au nombre de noyaux 218Po, est comparable à celle des autres noyaux. En déduire que la contribution du polonium 218 à la radioactivité de l'échantillon introduit plus tard dans le détecteur peut être négligée. L'activité initiale de chaque type de noyaux est identique. La demi-vie du plomb 214 est 27 min ; celle du bismuth 214 est 20 min. Au bout de 10 min, le nombre de noyaux de polonium 218 présents dans l'échantillon est 8 fois plus petit que le nombre initial de noyaux ; au bout de 12 min, 16 fois plus petit que le nombre initial. Par contre le nombre initiaux de noyaux de plomb 214 et de bismuth 214 n'ont même pas été divisés par deux. La contribution du polonium 218 est donc négligeable. Ayant pris soin de ne pas soulever les poussières déposées depuis très longtemps dans le local où l'air ambiant est aspiré, on admettra que le plomb 210 ne participe pas à la radioactivité de l'échantllon recueilli, ni ses descendants. Quels sont les euls noyaux radioactifs émetteurs b- qui contribuent à la radioactivité mesurée par le détecteur ? plomb 214 et de bismuth 214. Evolution temporelle : On se propose d'étudier l'évolution temporelle d'une population de noyaux radioactifs de plomb 214. Loi de décroissance. Rappeler l'expression mathématique de l'évolution temporelle du nombre N d'une population de noyaux de constante radioactive l. N(t) = N0 exp(-lt). On rappelle que le nombre de désintégrations par seconde d'une population de noyaux radioactifs est définie par l'activité ( en becquerels Bq) : A = - dN(t) / dt. En déduire que la realtion entre l'activité et le nombre de noyaux est : A(t) = l N. dériver par rapport au temps : N(t) = N0 exp(-lt). dN(t) / dt = N0(-l) exp(-lt). -dN(t) = A = l N0 exp(-lt) =l N . En utilisant la figure ci-dessous, comparer graphiquement et sans calcul l'activité de la population de plomb 214 aux instants de dates t1 = 25 min et t2 = 50 min. Justifier.
t2-t1 est proche de la demi-vie du plomb 214 : à chaque demi-vie le nombre de noyaux radioactifs initiaux est divisé par 2. L'activité du plomb 214 est divisée par deux entre les dates t1 et t2.
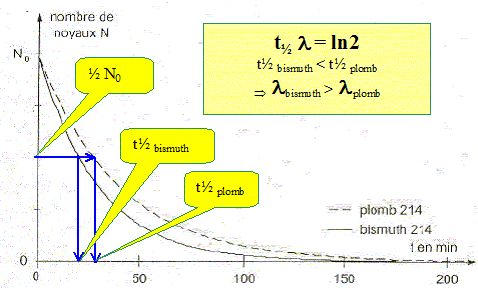
A partir de la figure ci-dessus et sans calculs, comparer l'activité de ½N0 noyaux de plomb 214 à celle du même nombre de noyaux de bismuth 214. En déduire lequel de ces deux radioéléments a la constante radioactive la plus grande.
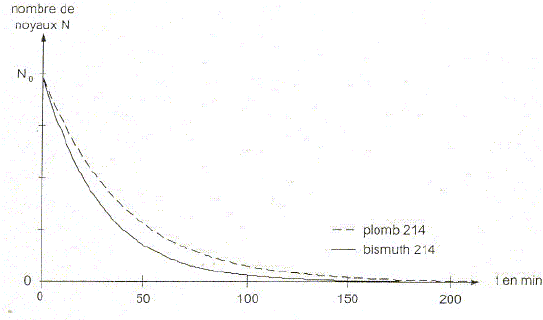
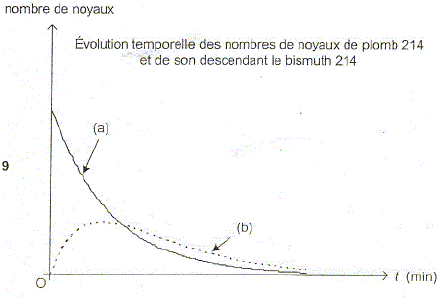
La figure ci-dessous représente l'évolution temporelle des nombres de noyaux d'un même échantillon renfermant à la fois des noyaux de plomb 214 et les noyaux de bismuth 214 descendants des noyaux de plomb qui se désintègrent.
Identifier les deux noyaux ( plomb 214 et bismuth 214) correspondant aux courbes a et b. Justifier en décrivant l'évolution temporelle de la courbe b. courbe a : plomb 214. Cette courbe traduit la décroissance exponentielle du nombre de noyaux de plomb 214. courbe b : bismuth 214. Au début, du fait de la désintégration d'un grand nombre de noyaux de plomb 214, le nombre de noyaux fils ( bismuth 214 ) augmente rapidement. Puis, du fait de la désintégration radioactive du bismuth 214, le nombre de noyaux de bismuth 214 va décroître. Indiquer en justifiant, quelle est l'équation différentielle qui régit dans ces conditions l'évolution temporelle du nombre de noyaux de bismuth 214.
(1) traduit l'évolution temporelle d'une population de N noyaux radioactifs de bismuth ( loi de décroissance radioactive) sans prendre en compte la formation du bismuth 214. (3) à gauche du signe "égal" on lit NBi et à droite on lit - NPb : le signe "moins" n'a aucun sens physique. (2) le terme -lBiNBi traduit la décroissance radioactive du Bismuth 214 et le terme lPbNPbtraduit la formation du Bismuth 214 par désintégration radioactive du plomb 214.
|
||||||
|
au |
||||||
|
|