|
bac S Liban 2007 : la station spatiale internationale à l'heure atomique Pharao, lois de Kepler, physique quantique d'après http://www.cpf.edu.lb/sphysique/ |
|||
|
|||
|
La station spatiale internationale (Internationale Space station, ISS) est le résultat d'une coopération internationale sans précédent qui va permettre, pendant plus de 10 ans, d'effectuer des expériences dans de nombreux domaines scientifiques. Lorsqu'elle sera achevée, l'ISS sera la plus grande structure jamais réalisée par l'homme dans l'espace. La surface de cet immense complexe de plus de 100 m de long sera équivalente à celle d'un grand stade de football comprenant des laboratoires, un module d'habitation… Le lancement du 1er élément de l'ISS, le module russe Zarya, a eu lieu en 1998 et, depuis novembre 2000, deux ou trois spationautes occupent en permanence la station. Sa construction se poursuit au fur et à mesure des vols de la navette spatiale américaine. L'horloge atomique Pharao (projet d'horloge atomique par refroidissement d'atomes en orbites), sera embarquée à l'horizon 2010 à bord de l'ISS. A la clé, de nouveaux tests en physique fondamentale. Cet instrument unique doit mesurer le temps avec une exactitude et une stabilité inégalées : l'horloge ne perdra qu'une petite seconde toutes les 300 millions d'années. D'après le site du CNES (mars 2006)
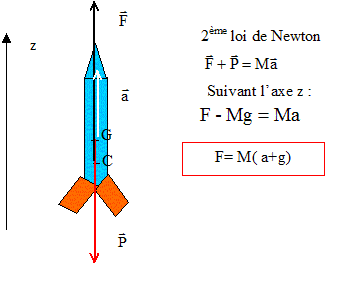
Le vecteur accélération est égale à la variation du vecteur vitesse divisée par la durée de cette variation. Ici tous les vecteurs sont colinéaires et de même sens ( la verticale ascendante) d'où : a =(v5-v4) / (t5-t4) = (25-14) / 2 ; a=5,5 m/s2. Valeur de la poussée.
Exprimer la masse en kg : M = 2,0 106 kg. F= 2,0 106 (10+5,5) = 3,1 107 N.
Par rapport au référentiel géocentrique, la station S effectue seize révolutions par jour sur une orbite circulaire, inclinée de 51,6° par rapport à l'équateur et située à une altitude z (environ 400 km). Données : M : masse de la Terre ; R : rayon de la Terre ; m : masse de la station ; G : constante de gravitation universelle ; z : altitude de la station On posera r = R+z. La Terre a une répartition de masse à symétrie sphérique et la station a des dimensions faibles par rapport à la distance qui la sépare de la Terre.
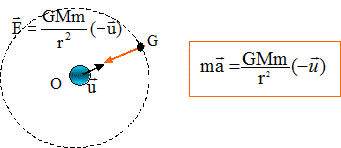
Etude de la vitesse : Dans le référentile géocentrique : La seule force exercée sur la station est la force centripète de gravitation ; la vitesse est portée par la tangente à la trajectoire circulaire au point considéré. La force et la vitesse sont donc perpendiculaires. Le travail de cette force est donc nul. d'après le théorème de l'énergie cinétique, l'énergie cinétique et en conséquence la vitesse sont constants : le mouvement est uniforme.
La vitesse est indépendante de la masse de la station : la vitesse de la station sur son orbite ne sera pas modifiée si la masse de celle-ci augmente. La 2ème loi de Kepler ou loi des aires s'énonce " le rayon vecteur joignant le centre de la planète à l'astre central décrit des surfaces équivalentes pendant des durées égales". En conséquence le mouvement circulaire d'un satellite est uniforme. Période de révolution T du satellite. Durée (s) nécessaire pour décrire une circonférence ( 2pr en mètre) à la vitesse v ( m/s) définie ci-dessus. 2pr = v T ; T= 2pr / v. Expression de T en fonction de G, M et r : Elever au carré l'expression de la période : T2 = 4p2 r 2 / v2. Remplacer v2 par son expression GM/ r : T2 = 4p2 r 3 / (GM). T = 2p[r 3 / (GM)]½. Satellite géostationnaire : La trajectoire du satellite est située dans le plan équatorial de la terre ; le satellite tourne dans le même sens que la terre et avec la même vitesse angulaire. L'altitude du satellite est voisine de 36 000 km. Pour un observateur terrestre, le satellite paraît immobile. "une orbite circulaire, inclinée de 51,6° par rapport à l'équateur" : la station n'est donc pas géostationnaire.
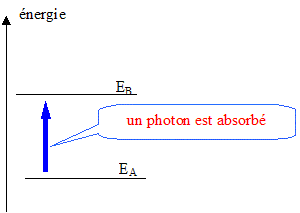
Depuis 1967, c'est l'horloge atomique au césium qui sert à définir la seconde. Cet appareil utilise les principes de la mécanique quantique : dans un atome, les niveaux d'énergie sont quantifiés. Cette horloge comprend un oscillateur à quartz. Le signal électrique oscillant est utilisé pour générer une onde électromagnétique de fréquence n = 9 192 631 770 Hz dans la cavité où on fait passer des atomes de césium 133. Si la quartz oscille à la bonne fréquence, les atomes absorbent le rayonnement et passent d'un niveau d'énergie EA au niveau d'énergie EB. Si la quartz se dérègle, ce n'est plus le cas et un système électronique agit sur la fréquence d'oscillation du quartz jusqu'à ce que les atomes absorbent à nouveau le rayonnement. Données : utiliser les valeurs arrondies ci-dessous pour les calculs. Constante de Planck : h = 6,63 10-34J.s ˜ 7 10-34 J.s Célérité de la lumière dans le vide et dans l'air : c = 299 792 458 m.s-1 ˜ 3 108 m.s-1 n = 9 192 631 770 Hz ˜ 9 109 Hz Expliquer la phrase : " dans un atome les niveaux d'énergie sont quantifiés ". Calculer la longueur d'onde de l'onde électromagnétique émise. Calculer la différence d'énergie entre les niveaux A et B de l'atome de césium 133. Sur un diagramme, placer les niveaux d'énergie EA et EB puis représenter la transition effectuée par les atomes de césium qui absorbent l'onde. Niveaux d'énergie : Seul un petit nombre de valeurs sont possibles pour l'énergie d'un atome : on dit " les niveaux d'énergie sont quantifiés". Longueur d'onde de l'onde électromagnétique émise : l = c/n = 3 108 / 9 109 = 3/90 = 1/30 = 3,3 10-2 m. Différence d'énergie entre les niveaux A et B de l'atome de césium 133 : DE = hn = 7 10-34 * 9 109 = 6,3 10-24 J. "les atomes absorbent le rayonnement et passent d'un niveau d'énergie EA au niveau d'énergie EB"
|
|||
|
|
|||
|
|
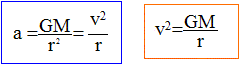 v = (GM/r)½.
v = (GM/r)½.