Aurélie 16/04/07
 

bac Inde 2007 : oscillateur mécanique horizontal ; amortissement (4 pts)

lycée-francais-pondichery

Google

Un pendule élastique est constitué d'un mobile de masse m =80 g pouvant se déplacer surun banc à coussin d'air horizontal. Ce mobile est attaché à un point fixe par un ressort de masse négligeable à spires non jointives, de raideur k. La position du mobile est repérée par l'abscisse x. A l'équilibre, la position du centre d'inertie G coïncide avec O, origine des abscisses.

 

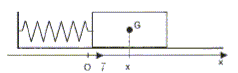
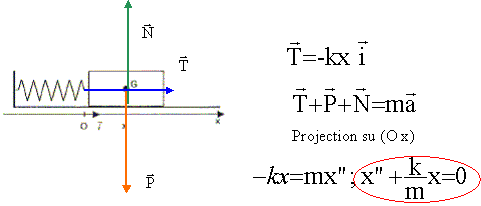
I. Oscillateur non amorti : on considère que les forces de frotements sont nulles.

  1. Indiquer l'expression vectorielle de la force F de rappel du ressort en fonction de l'abscisse x.
  2. Faire l'inventaire des forces qui s'exercent sur le mobile et les représenter sur un schéma.
  3. A l'aide de la seconde loi de Newton, établir l'équation différentielle du mouvement.
  4. Un dispositif d'enregistrement de la position x du mobile permet de mesurer la valeur T0 de la période du mouvement T0 = 0,20 s. Quelle est la valeur de la raideur k du ressort sachant que T0 = 2p(m/k)½ ?

II. Oscillateur amorti :

Le dispositif est modifié et les frottements deviennent plus importants. L'équation différentielle du mouvement a maintenant l'expression suivante :

a+a v + b x=0 avec a = d2x/dt2 et v = dx/dt
  1. A l'aide de l'analyse dimensionnelle déterminer les unités de a et b dans le système internationnal.
    On a pu déterminer que a = 60 S.I et b =1,00 103 S.I.
  2. La méthode numérique d'Euler permet de résoudre cette équation différentielle. Un extrait de la feuille de calcul est représentée ci-dessous :
    instant t (s)
    accélération (m/s2)
    vitesse v (m/s)
    abscisse x (m)
    0
    0,00
    -30,0
    0,00
    0,030
    1
    0,01
    -9,0
    -0,30
    0,027
    2
    0,02
    0,3
    -0,39
    0,023
    3
    0,03
    4,0
    -0,39
    0,019
    4
    0,04
    5,1
    -0,35
    0,016
    5
    0,05
    5,0
    -0,30
    0,013
    6
    0,06
    4,5
    -0,25
    0,010
    7
    0,07
    a7
    -0,20
    0,008
    8
    0,08

    v8
    x8
    Calculer a7 à l'instant t7 = 0,07 s à partir de l'équation différentielle.
  3. Calculer v8 et x8 à partir de la méthode d'Euler.
  4. Tracer la courbe donnant l'abscisse x en fonction du temps
  5. Quels sont les noms des deux régimes possibles d'un oscillateur ?
    La courbe permet -elle d'affirmer dans quel régime se trouve l'oscillateur ?
I. Oscillateur non amorti :

Valeur de la raideur k du ressort :

T0 = 2p(m/k)½ ; T02 = 4p2m/k ; k= 4p2m / T02 =4*3,142*0,08 / 0,22 =78,87 N/m ( réponse k=79 N/m).

a+a v + b x=0 avec a = d2x/dt2 et v = dx/dt

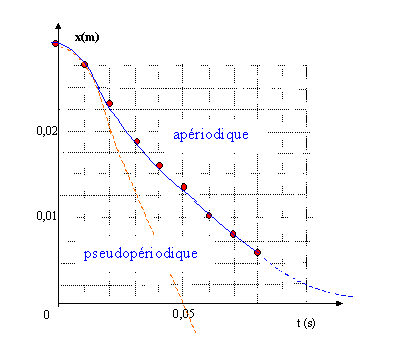
Unités de a et b dans le système internationnal :

b x a la dimension d'une accélération : longueur / temps 2 soit [b x]=L T-2.

x a la dimension d'une longueur soit [x]= L.

[b] =L T-2 / L ; [b] = T-2.

a v a la dimension d'une accélération : longueur / temps 2 soit [a v]=L T-2.

v a la dimension d'une vitesse : longueur / temps soit [v]= LT-1.

[a] =L T-2 /( LT-1) ; [a] = T-1.

Calcul de a7 à partir de l'équation différentielle :

a7= -(a v7 + b x7) avec v7 = -0,20 m/s et x7 = 0,008 m.

a7= -(60*(-0,20) + 103*0,008)= 4,0 m/s2.

Calcul de v8 et x8 à partir de la méthode d'Euler :

v8 -v7= a7 Dt avec D t = 0,01 s.

v8 =v7+ a7 Dt = -0,20 + 4*0,01 = -0,16 m/s.

x8 -x7= v7 Dt avec D t = 0,01 s.

x8 =x7+ v7 Dt = 0,008 -0,2*0,01 =0,006 m/s.

Courbe donnant l'abscisse x en fonction du temps et les deux régimes possibles d'un oscillateur amorti :

Dans le cas d'un régime pseudopériodique ( amortissement faible T voisin de T0 soit 0,20 s), à 0,25 T0, l'accélération et l'abscisse seraient nulles.

Le régime pseudopériodique faiblement amorti n'est pas compatible avec le graphe.

La courbe ne permet pas d'affirmer que l'oscillateur se trouve dans un régime apériodique ( la période T tend vers l'infini ) ou dans un régime pseudopériodique très fortement amorti.

 
 

retour -menu